В равнобедренном треугольнике ABC с основанием ав вершины ас и точка пересечения высот расположены на одной окружности радиус 5 найти площадь трехуг

Показать ответ

Ответ:

умник20072

20.11.2021 21:31

ответ: 8 пар.

Объяснение:

mn + n + 14 = (m-1)(m-1)

Раскрыв скобки, получаем:

mn + n + 14 = m^2 - 2m + 1

Перенесем слагаемые с переменными влево, а свободный член — вправо:

mn + n - m^2 + 2m = 1 - 14

mn + n - m^2 + 2m = -13

Из обеих частей уравнения вычтем :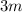

mn + n - m^2 + 2m - 3m= -13 - 3m

Разложим левую часть на множители методом группировки:

n(m+1)-m(m-2+3)= -13 - 3m

n(m+1)-m(m+1)= -13 - 3m

(m+1)(n-m)= -13 - 3m

К обеим частям уравнения прибавим выражение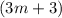 (3m+3) :

(m+1)(n-m) +3m + 3= -13 - 3m + 3m + 3

(m+1)(n-m) +3m + 3= -10

Вынесем общий множитель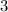 за скобки:

(m+1)(n-m) +3(m + 1)= -10

Вынесем (m+1) :

(m+1)((n-m) + 3)= -10

(m+1)(n-m + 3)= -10

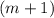Так значения m и n целые (по нужному условию), значения выражений в скобках не могут быть дробными.

Произведение двух целых чисел равно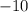 в восьми случаях:

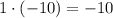1) $1\cdot(-10)=-10$ ;

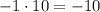2) $-1\cdot10=-10$ ;

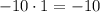3) $-10\cdot1=-10$ ;

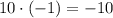4) $10\cdot(-1)=-10$ ;

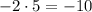5) $-2\cdot 5 = -10$ ;

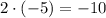6) $2\cdot (-5)=-10$ ;

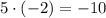7) $5\cdot (-2)=-10$ ;

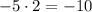8) $-5\cdot 2 = -10$ .

Определим, какие будут значения m и n, если значения выражений в скобках равны множителям из каждого случая:

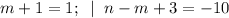
1) $m+1=1;\; \;| \; \; n-m+3=-10$

Получаем:

m=0

n-0+3=-10

n=-13

Значит, (m,n) = (0; -13).

Аналогично рассмотрим следующие случаи:

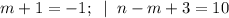
2) $m+1=-1;\; \;| \; \; n-m+3=10$

(m,n) = (-2; 5).

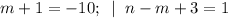
3) $m+1=-10;\; \;| \; \; n-m+3=1$

(m,n) = (-11; -13).

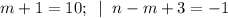
4) $m+1=10;\; \;| \; \; n-m+3=-1$

(m,n) = (9; 5).

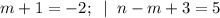
5) $m+1=-2;\; \;| \; \; n-m+3=5$

(m,n) = (-3; -1).

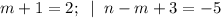
6) $m+1=2;\; \;| \; \; n-m+3=-5$

(m,n) = (1; -7).

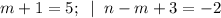
7) $m+1=5;\; \;| \; \; n-m+3=-2$

(m,n) = (4; -1).

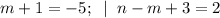
8) $m+1=-5;\; \;| \; \; n-m+3=2$

(m,n) = (-6; -7).

Выходит, 8 пар целых чисел (m, n) удовлетворяют данное равенство.

0,0(0 оценок)

Ответ:

Avetodor

25.12.2020 19:10

Задача решается просто. 3 взвешивания.

Сначала поделим 15 пополам. У нас две кучки по семь орехов плюс один лишний. Откладываем его в сторону. Кладем кучки на чаши весов. Если чаши останутся в равновесии, значит гнилой тот орех, который мы отложили. Однако если одна чаша перевесила другую, мы берем более легкую кучку и снова делим пополам. У нас две кучки по три плюс один лишний орех. Откладываем его в сторону. Кладем кучки на весы. Если чаши остались в равновесии, гнилой орех тот, что лежит в стороне. Но если опять одна из чаш снова перевешивает, значит снимаем легкую кучу и... Правильно! Снова делим пополам и откладываем один лишний. теперь все элементарно. Чаши в равновесии, значит глиной орех отложен в сторону. Ну а если одна перевесила другую, то гнилой орех в более легкой чашке. Поэтому мы ограничились тремя взвешиваниями. Это единственное правильное решение.

Как говориться логика она везде. Обращайся если будут еще такие задачи...

0,0(0 оценок)

Популярные вопросы: Математика