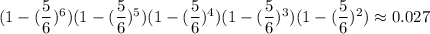в школе 40% учеников изучают немецкий язык 76% изучают английский язык и 25% изучающих английский язык изучают также и немецкий язык Какой процент учеников школы они изучают английский и немецкий
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда
Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна - это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
5378 − пять тысяч триста семьдесят восемь.
5 единиц класса тысяч, 3 сотни класса единиц, 7 десятков класса единиц и 8 единиц класса единиц.
Всего в нем 5378 единиц, 57 десятков, 53 сотни, 5 тысяч.
32609 − тридцать две тысячи шестьсот девять.
3 десятка класса тысяч, 2 единицы класса тысяч, 6 сотен класса единиц и 9 единиц класса единиц.
Всего в нем 32609 единиц, 3260 десятков, 326 сотен, 32 тысячи и 3 десятка тысяч.
940615 − девятьсот сорок тысяч шестьсот пятнадцать.
9 сотен тысяч, 4 десятка тысяч, 6 сотне единиц, 1 десяток единиц, 5 единиц единиц.
Всего в нем 940615 единиц, 94061 десятков, 9406 сотен, 940 тысяч, 94 десятков тысяч.
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда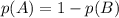
Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна
(среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна 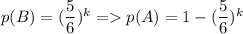 - это и есть искомая вероятность в данной задаче.
- это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна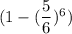 . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна
. При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 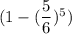 . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна 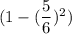
Тогда искомая вероятность