В спортзале было 64 меча ⅜ всех мечей составляли волейбольные мечи а боскетюольных в 4 раза больше а остальные футбольные мечи

а) 1/36

б) 7/8

Пошаговое объяснение:

а) При бросании первой игральной кости общее количество исходов равно 6. Только при одном исходе выпадет число 5. Значит вероятность такого события равна 1/6.

При бросании второй игральной кости общее количество исходов равно 6. При двух исходах выпадет число большее, чем 4 (т.е. 5 и 6). Значит вероятность такого события равна 2/6=1/3.

При бросании третьей игральной кости общее количество исходов равно 6. При трех исходах выпадет нечетное количество очков (т.е. 1, 3 и 5). Значит вероятность такого события равна 3/6=1/2.

Осталось перемножить полученные вероятности.

Получим 1/6 * 1/3 * 1/2 = 1/36 - искомая вероятность события.

б) Бросают три игральные кости. Общее количество исходов  n=6*6*6=216

Событие А - "хотя бы на одной кости выпало четное количество очков".

Противоположное ему событие ¬А - "ни на одной кости не выпало четное количество очков". m- число исходов, благоприятствующих наступлению события ¬A. m=3*3*3=27

Значит, вероятность Р(¬А)= m/n = 27/216 = 1/8

Искомая вероятность Р(А)= 1-Р(¬А) = 1-1/8 = 7/8

1.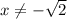   и x≤−1  и 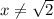и  x≥1

2.  x=0

Пошаговое объяснение:

Заменим 2²⁻ˣ² -1 = y и приравняем к 0

3/y² - 4/y+1=0 (грубо говоря, умножим обе части на y² и получаем квадратное уравнение)

y²-4y+3=0   D=4   y₁=1   y₂=3

подставляем  y₁     2²⁻ˣ² -1 = 1   2²⁻ˣ²= 2  => 2-x²=1     x²=1  т.е. x₁= -1   x₂= 1

подставляем  y₂    2²⁻ˣ² -1 = 3   2²⁻ˣ²=2²  => 2-x²=2   x²=0  т.е. x₃= 0

Так же обращаем внимание, что 2²⁻ˣ² -1 не может быть равен 0 т.е.

2²⁻ˣ² -1≠0   2²⁻ˣ² ≠ 2⁰ => 2-x²≠0   x²≠2  т.е.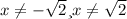    

Все собираем в кучу и получаем то что в ответе