В стране 201 город, из каждого выходит ровно 10 дорог, причем из любого города можно доехать до любого другого. Докажите, что можно выбрать 20 городов, никакие два из которых не соединены дорогой

Показать ответ

Ответ:

Lichnosti

27.12.2020 02:21

Пошаговое объяснение:

2х+3=х-6

2х-х=-6-3

х=-9

Проверка: 2*(-9)+3=-9-6

-18+3=-15

-15=-15 Верно!

ответ: -9.

-----------------------------------------

z+4-3=2z

z-2z=-4+3

-z=-1

z=1

Проверка: 1+4-3=2*1

5-3=2

2=2 Верно!

ответ: 1.

-----------------------------------------

5-3y=4-2y

-3y+2y=4-5

-y=-1

y=1

Проверка: 5-3*1=4-2*1

5-3=4-2

2=2 Верно!

ответ: 1.

-----------------------------------------

7-3х=4х-9

-3х-4х=-9-7

-7х=-16

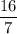
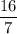х= $\displaystyle \frac{16}{7}$

Проверка:

$\displaystyle 7-3*\frac{16}{7}=4*\frac{16}{7} -9$

$\displaystyle 3*\frac{16}{7} =\frac{3*16}{7} =\frac{48}{7}$

$\displaystyle 7 -\frac{48}{7} =\frac{7}{1} -\frac{48}{7} =\frac{7*7-48*1}{7} =\frac{49-48}{7} =\frac{1}{7}$

///////

$\displaystyle 4*\frac{16}{7} =\frac{4*16}{7} =\frac{64}{7}$

$\displaystyle \frac{64}{7} -9=\frac{64}{7} -\frac{9}{1} =\frac{64*1-9*7}{7} =\frac{64-63}{7} =\frac{1}{7}$

$\displaystyle \frac{1}{7} =\frac{1}{7}$ Верно!

ответ: $\displaystyle \frac{16}{7}$ .

-----------------------------------------

6а-1=3а+7

6а-3а=7+1

3а=8

а= $\displaystyle \frac{8}{3}$

Проверка:

$\displaystyle 6*\frac{8}{3}-1=3*\frac{8}{3} +7$

$\displaystyle 6*\frac{8}{3} =\frac{6*8}{3} =\frac{48}{3} =16$

16-1=15

///////

$3*\frac{8}{3} =\frac{3*8}{3} =\frac{24}{3} =8$

8+7=15

15=15 Верно!

ответ: $\displaystyle \frac{8}{3}$ .

-----------------------------------------

10y-3=5+3y

10y-3y=5+3

7y=8

y= $\displaystyle \frac{8}{7}$

Проверка:

$\displaystyle 10*\frac{8}{7}-3=5+3*\frac{8}{7}$

$\displaystyle 10*\frac{8}{7} =\frac{10*8}{7} =\frac{80}{7}$

$\displaystyle \frac{80}{7} -3=\frac{80}{7} -\frac{3}{1} =\frac{80-3*7}{7} =\frac{80-21}{7} =\frac{59}{7}$

///////

$\displaystyle 3*\frac{8}{7} =\frac{3*8}{7} =\frac{24}{7}$

$\displaystyle 5+\frac{24}{7} =\frac{5}{1} +\frac{24}{7} =\frac{5*7+24*1}{7} =\frac{35+24}{7} =\frac{59}{7}$

$\displaystyle \frac{59}{7} =\frac{59}{7}$ Верно!

ответ: $\displaystyle \frac{8}{7}$ .

0,0(0 оценок)

Ответ:

мальчуган2

27.12.2020 02:21

1) 2х + 3 = х - 6, 2) z + 4 - 3 = 2z, 3) 5 - 3y = 4 - 2y,

2х - х = -6 - 3, z - 2z = -1, -3у + 2у = 4 - 5,

х = -9; -z = -1, -у = -1,

z = 1; у = 1;

4) 7 - 3x = 4x - 9, 5) 6a - 1 = 3a+ 7, 6) 10y - 3 = 5 + 3y,

-3х - 4х = -9 - 7, 6а - 3а = 7 + 1, 10у - 3у = 5 + 3,

-7х = -16, 3а = 8, 7у = 8,

х = 16/7, а = 8/3, у = 8/7,

х = 2 целые 2/7; а = 2 целые 2/3; у = 1 целая 1/7.

0,0(0 оценок)

Популярные вопросы: Математика

1978dan

05.01.2020 18:39

Начертите горизонтальную прямую и отметьте на ней точку с. правее течки с на расстоянии 5 см отметьте точку d. отметьте точку о – начало отсчета, если c( -2), а d( 3 )....

oldespower

05.01.2020 18:39

Гимнастика выбрали 12 коротышек бокс на 4 меньше чем в россии по футболу на 5 больше чем букв сколько занималась спортом предпочитают коротышки...

ПрофессиАНАЛ

05.01.2020 18:39

Основание равнобедренного треугольника равно 2,4дм.боковая сторона равна 2/3 длины основания.найдите периметр этого треугольника...

Bazzaevat

05.01.2020 18:39

Дедушке 56 лет, его сыну 32 года, внукам 11 и 7 лет. через сколько лет возраст дедушки будет давление сумме возраста его сына и внуков?...

terrrylook31

05.01.2020 18:39

Составить квадратное уравнение, если его корни x1=10, x2=12 через дискриминант ((...

podzolkova54

05.01.2020 18:39

Начертите координатный луч, единичный отрезок которого равен 3 см. отметьте на нём точки а (1); в (2); с (1/6); d (1 5/6); е (2 1/3); f (1.5)....

kapov2017p0aak6

31.03.2020 17:01

Решите уравнение 25-4x=12-5x 6 класс...

Катюшка311001

31.03.2020 17:01

Найдите значение выражения 1 \14 • y+ 8\21•y- 3\35•y ,если y =1 4\11...

Denchik15070

31.03.2020 17:01

1. у класі 32 учні. 7/8 з них були в театрі. скільки учнів відвідали театр? 2. у класі 12 учнів брали участь в олімпіаді, що становить 3/7 всього класу. скільки учнів...

Trollyz

31.03.2020 17:01

Составь выражения и найди их значения: в два магазина 60 одинаковых ящиков винограда, причём в первый магазин 420 кг, а во второй- 300 кг.сколько килограммов винограда...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку