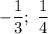Первая четверть XVII столетия в России ознаменовалась преобразованиями, непосредственно связанными с "европеизацией" страны. Начало Петровской эпохи сопровождалось серьезными изменениями в нравах и быту. Коснулись преобразования просвещения и других сфер общественной жизни. активное проникновение западноевропейских ценностей отмечалось в стране на протяжении всего XVII столетия. Однако направленность этого влияния изменила именно Петровская эпоха. Век XVIII стал периодом внедрения новых ценностей и идей. Ключевым объектом преобразований стала жизнь русского дворянства. Указ 1705 г. обязал всех мужчин, кроме священников и монахов, сбрить усы и бороду. Таким образом, общество оказалось разделено на 2 неравные части. Одна – дворянство и элита городского населения, которая находилась под давлением европеизации, другая же сохраняла привычный уклад.Преобразования государя позволили стране выйти на качественно новый уровень. В первую очередь существенно сократилось отставание культурной и экономической сфер от передовых стран Европы. Кроме этого, Россия стала превращаться в великую и могущественную державу. За счет внедрения европейских ценностей страну стали воспринимать на международной арене. Благодаря петровским реформам теперь ни одно важное событие не решалось без участия России. Изменения, которые произошли в жизни государства в первой четверти 18 столетия, были весьма прогрессивными. Однако они еще сильнее увеличили разрыв между дворянством и низшими классами. Петр провел колоссальную работу в стране. Несмотря на то что он не учитывал многие обстоятельства и особенности русского менталитета, историки признают, что государство в период его правления сделало огромный шаг вперед. Общество стало прогрессивным, светским, воспитанным, образованным. У потомков Петр Первый, можно сказать, практически единственный правитель, который сохранил титул Великий, дарованный ему еще при жизни.
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена:
Подставим в корень уравнения и получим:
— неправда
Подставим в корень уравнения и получим:
— неправда
Подставим в корень уравнения и получим:
— правда
Следовательно, — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на (см. вложение).
После этого исходное уравнение можно записать разложив на множители:
Имеем многочлен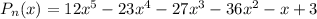
Корнями многочлена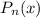
называют корни уравнения
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена:
Подставим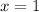
в корень уравнения и получим:
Подставим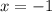
в корень уравнения и получим:
Подставим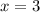
в корень уравнения и получим:
Следовательно,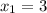
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на 
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
Решаем второе уравнение:
Рациональные корни: