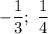1) 20,7 : 0,9 = 207 : 9 = 23 2) в порядке убывания 1,437; 1,4302; 1,43. 3) х + (х - 0,2) = (2х - 0,2) кг картофеля в двух мешках. 4)число 100 составляет 100% число 13 составляет х% х=13·100:100=13% О т в е т. 13% составляет число 13 от числа 100. 5) 28 т= 28 000 кг 28 000 :100 ·18= 5040 кг свеклы продали до обеда. 28 000 - 5040 = 22960 кг свеклы осталось продать
6)18 работающих женщин составляют 45% х рабочих составляют 100% х = 18·100 :45=40 рабочих в цехе? 7)В 1 кг сливок 250 г жиров 1 кг= 1000 г 1000 г составляет 100% 250 г составляет х % х=250·100:1000=25% О т в е т. 25 % жирности сливок, в 1 кг которых содержится 250 г жиров
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена:
Подставим в корень уравнения и получим:
— неправда
Подставим в корень уравнения и получим:
— неправда
Подставим в корень уравнения и получим:
— правда
Следовательно, — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на (см. вложение).
После этого исходное уравнение можно записать разложив на множители:
1,437; 1,4302; 1,43.
3) х + (х - 0,2) = (2х - 0,2) кг картофеля в двух мешках.
4)число 100 составляет 100%
число 13 составляет х%
х=13·100:100=13%
О т в е т. 13% составляет число 13 от числа 100.
5) 28 т= 28 000 кг
28 000 :100 ·18= 5040 кг свеклы продали до обеда.
28 000 - 5040 = 22960 кг свеклы осталось продать
6)18 работающих женщин составляют 45%
х рабочих составляют 100%
х = 18·100 :45=40 рабочих в цехе?
7)В 1 кг сливок 250 г жиров
1 кг= 1000 г
1000 г составляет 100%
250 г составляет х %
х=250·100:1000=25%
О т в е т. 25 % жирности сливок, в 1 кг которых содержится 250 г жиров
Имеем многочлен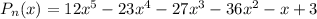
Корнями многочлена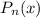 называют корни уравнения
называют корни уравнения
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: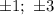
Подставим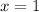 в корень уравнения и получим:
в корень уравнения и получим:
Подставим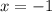 в корень уравнения и получим:
в корень уравнения и получим:
Подставим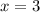 в корень уравнения и получим:
в корень уравнения и получим:
Следовательно,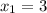 — один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на  (см. вложение).
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
Решаем второе уравнение:
Рациональные корни: