В треугольника ABC проведены медианы AP, BQ и CR. Найдите сумму AQ+CP+BR если периметр треугольника ABC равен 58,4см​

1) Допустим, он спросил у рыцаря. Рыцарь дал верный ответ: "Да. Среди нас хотя бы один - рыцарь". Но тут возникает неоднозначность, потому что второй может быть как рыцарем, так и лжецом, поскольку первый рыцарь, и уже выполняется условие, что среди них хоть кто-то рыцарь.
2) Допустим, он спросил у лжеца. Если лжец ответил: "Да, среди нас есть рыцарь", то среди них нет рыцаря. То есть второй - тоже лжец.
Если лжец ответил: "Нет, среди нас нет рыцарей", то среди них есть рыцарь. Это второй островитянин.
Если автор получил, что хотел, то ему подходит пункт 2. То есть первый лжец, а в зависимости от его ответа второй либо рыцарь, либо тоже лжец.

Но, возможно, это не всё решение задачи. Следует еще подумать над тем, а не являются ли эти островитяне единственными, кто населяет остров

Пошаговое объяснение:

1. Так как слагаемые относятся как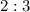 , то второе слагаемое в 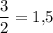раза больше первого. Если первое слагаемое максимальное (99), то второе не превышает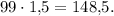

Таким образом,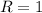 , , 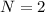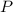— четная цифра.

Кроме того, в результате умножения первого слагаемого на 1,5 получается трехзначное число. Значит первое слагаемое не меньше

Таким образом, первое слагаемое 88, .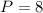

Отсюда , .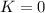

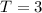2. Так как правые части пропорций равны, то равны и их левые части:

Так как условие задачи не указывает, какой знак имеют числа, то каждое из утверждений задачи в общем случае не верно.

а) неравенство верно только при отрицательных значениях ;

б) равенство верно только при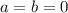 , но тогда в пропорции появляются отношения вида ;

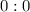в) необязательно, возможно и равенство .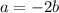

Если точно известно, что числа положительны, то правильное утверждение — в).