Пусть a = x - d, b = x, c = x + d, где d - разность прогрессии. Известно,
что SΔ = , где Р - периметр треугольника; по условию R•г = 130
⇒ R = 130/r ⇒ abc·r/(4·130) = (a + b + c)·r/2 ⇒ abc = 260·(a + b + c) ⇒
(x - d)·x·(x + d) = 260·(x - d + x + x + d) ⇔ x(x² - d²) = 3·260x ⇒
x(x² - d² - 780) = 0 ⇒ x² = d² + 780, так как сторона Δ положительна.
По условию (а, b, с) – тройка целых чисел ⇒ подбираем d так, чтобы было целым и наименьшим из возможных;
при d = 2 имеем: х = = 28 ⇒ a = 28 - 2 = 26; b = 28; c = 28 + 2 = 30
⇒ (26; 28; 30) – наименьшая целая тройка сторон треугольника.
Пусть a = x - d, b = x, c = x + d, где d - разность прогрессии. Известно,
что SΔ =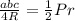
, где Р - периметр треугольника; по условию R•г = 130
⇒ R = 130/r ⇒ abc·r/(4·130) = (a + b + c)·r/2 ⇒ abc = 260·(a + b + c) ⇒
(x - d)·x·(x + d) = 260·(x - d + x + x + d) ⇔ x(x² - d²) = 3·260x ⇒
x(x² - d² - 780) = 0 ⇒ x² = d² + 780, так как сторона Δ положительна.
По условию (а, b, с) – тройка целых чисел ⇒ подбираем d так, чтобы
было целым и наименьшим из возможных;
при d = 2 имеем: х =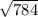
= 28 ⇒ a = 28 - 2 = 26; b = 28; c = 28 + 2 = 30
⇒ (26; 28; 30) – наименьшая целая тройка сторон треугольника.