В треугольнике ABC стороны AB и AC равны, угол А равен 68°. Биссектрисы углов В и С пересекаются в точке М. Найдите величину угла ВМС. ответ дайте в градусах.
Запишите решение и ответ.
​

Если мы ищем производную по х то ответ будет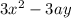

Если мы ищем производную по у то ответ будет

Если мы берём производную по а то ответ будет просто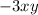

Так же производную невозможно искать если приравнивать к нулю.

Рассчитывал производную  по основной формуле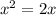 . Если мы берём производную от степени то уменьшаем её на 1 и выносим изначальное число степени перед иксом.

А так же если у мы берём допустим по х то там где просто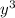  то это равно 0 и мы не учитываем, а если есть х и у то смотрим на степень х и у и действуем по схеме выше. Так как у нас в конце стоит 3ху и х и у в первой степени, то мы просто убираем либо х либо у, и оставляем либо х либо у.

Пошаговое объяснение:

Sполн=2Sосн+Sбок

Sосн=a^2*sqrt{3}/4, где а-длина ребра призмы

Sбок=3а^2, т.к. все три боковые стороны-квадраты со стороной а.

Sполн=2*a^2*sqrt{3}/4 + 3а^2 = a^2*sqrt{3}/2 + 6а^2/2=

        a^2(sqrt{3}+6)/2

Sполн=4+8sqrt{3} (по условию)

        a^2(sqrt{3}+6)/2=4+8sqrt{3}

        a^2=2*4(1+2sqrt{3})/(sqrt{3}+6)

        a^2=8(1+2sqrt{3})/(sqrt{3}+6)

Sосн=a^2 sqrt{3}/4=8(1+2sqrt{3})*sqrt{3}/(4(sqrt{3}+6))=

                            =2sqrt{3}(1+2sqrt{3})/(sqrt{3}+6)=

                            =2(sqrt{3}+2*3)/(sqrt{3}+6)=

                            =2(sqrt{3}+6)/(sqrt{3}+6)=2

ответ: 2