Пусть X и Y - какие-то множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с функции y = f(x) множество X отображается в множество Y. Поэтому функцию называют также отображением.
Например, авиапассажиры сидят в креслах салона пассажирского самолёта. Пусть X - множество пассажиров, а Y - множество кресел салона. Тогда возникает соответствие f : каждому пассажиру x∈X сопоставляется то кресло y = f(x), в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью определения которой является множество X пассажиров, а областью значений - множество f(X) занимаемых ими кресел. Если заполнены не все кресла Y, то множество значений функции будет подмножеством Y, не совпадающим со всем множеством Y.
Если в кресле находятся два пассажира и (например, мать и ребёнок), то это никак не противоречит определению функции f, которая и , и однозначно ставит в соответствие кресло . При этом такая функция принимает одно и то же значение при разных значениях и аргумента, подобно тому как числовая функция y = f(x) = x² принимает одно и то же значение 9 при x = - 3 и при x = 3.
Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.
В математическом анализе часто X обозначают как D (область определения функции), а Y как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел). На сайте есть урок Как найти область определения функции.
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от икса или f(x). И это неслучайно. Функции составляют бОльшую часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и L = {l, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.
Решение. Итак, множество A содержит 5 элементов, а множество L - 3 элемента. Если мы поставим стрелки, ведущие от каждого элемента множества L к элементам множества A, то некоторым элементам L будут соответствовать более одного элемента A. Такое соответствие не является функцией по определению. Но если мы проведём стрелки от элементов A к элементам L, то некоторым элементам A будут соответствовать одни и те же элементы L, но при этом каждому элементу A будет соответствовать не более одного элемента L. Такое соответствие не противоречит определение функции, следовательно, ответ на вопрос задания - положительный.
Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией:
Пошаговое объяснение:
1) определим тип кривой и приведем к каноническому виду.
y² - 2y + 3x - 3 = 0
Приводим квадратичную форму
B = y²
к главным осям, то есть к каноническому виду.
матрица этой квадратичной формы:
0 0
0 1
находим собственные числа и собственные векторы этой матрицы:
(0 - λ)x₁ + 0y₁ = 0
0x₁ + (1 - λ)y₁ = 0
характеристическое уравнение:
итак, мы имеем параболу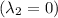
обшее уравнение канонического вида
(y - y₀)² = 2p(x - x₀)
выделим в нашем уравнении полный квадрат для у
(y² -2y +1) +3x -3 -1 =0
(y-1)² = -3x -4
теперь нам надо справа выделить 2р и (х -х₀)
(y-1)² = 2*(-3/2)(x -4/3) - это и есть канонический вид заданного уравнения
теперь точки пересечения
мне удобнее решать систему
із второго выразим х и подставим в первое
x = -y -1
y²-2y+3(-y-1) -3=0; y² -5y -6 = 0; ⇒ y₁ = 6; y₂= -1 ⇒ х₁ = -6-1=-7; х₂ = -(-1)-1 =0
вот это получились наши точки пересечения
М₁(-7;6) М₂(0; -1)
Пошаговое объяснение:
Пусть X и Y - какие-то множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с функции y = f(x) множество X отображается в множество Y. Поэтому функцию называют также отображением.
Например, авиапассажиры сидят в креслах салона пассажирского самолёта. Пусть X - множество пассажиров, а Y - множество кресел салона. Тогда возникает соответствие f : каждому пассажиру x∈X сопоставляется то кресло y = f(x), в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью определения которой является множество X пассажиров, а областью значений - множество f(X) занимаемых ими кресел. Если заполнены не все кресла Y, то множество значений функции будет подмножеством Y, не совпадающим со всем множеством Y.
Если в кресле находятся два пассажира и (например, мать и ребёнок), то это никак не противоречит определению функции f, которая и , и однозначно ставит в соответствие кресло . При этом такая функция принимает одно и то же значение при разных значениях и аргумента, подобно тому как числовая функция y = f(x) = x² принимает одно и то же значение 9 при x = - 3 и при x = 3.
Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.
В математическом анализе часто X обозначают как D (область определения функции), а Y как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел). На сайте есть урок Как найти область определения функции.
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от икса или f(x). И это неслучайно. Функции составляют бОльшую часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и L = {l, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.
Решение. Итак, множество A содержит 5 элементов, а множество L - 3 элемента. Если мы поставим стрелки, ведущие от каждого элемента множества L к элементам множества A, то некоторым элементам L будут соответствовать более одного элемента A. Такое соответствие не является функцией по определению. Но если мы проведём стрелки от элементов A к элементам L, то некоторым элементам A будут соответствовать одни и те же элементы L, но при этом каждому элементу A будет соответствовать не более одного элемента L. Такое соответствие не противоречит определение функции, следовательно, ответ на вопрос задания - положительный.
Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией: