в урні 10 кульок, 3 червоних , 5 синіх , 2 білих. Яка ймовірність що з урни буде витягнуто синю кульку ​

Решение задачи и простое и одновременно не очень сложное.
Расчет приведен в таблице - в приложении.
В задаче ДВА случайных события.
Первое - выбрать случайное зерно. - p11 = 0.96, р21=0,02 и далее.
Второе - оказался случайный не брак (более 50= Качественное) - р21 = 0,5, р22=0,2 и далее.
Вероятность события  "И" - И 1с И Кач - равна ПРОИЗВЕДЕНИЮ вероятностей.
Вероятность события "ИЛИ" - варианты - равна СУММЕ вероятностей таких событий.
Все расчеты проверяются по формулам ПОЛНОЙ вероятности, которая всегда равна 1 = 100%.
И так получаем, (смотрим в таблицу расчета) 
Вероятность "хорошего" зерна - 49%, а "плохого" = 51%.
В сумме (по полной вероятности) = 100%. - и это правильно.
ОТВЕТ: Вероятность случайно выбрать "хорошее" зерно = 49%.
Далее - по формуле Байеса.
Вероятность, что это будет "хорошее" зерно 1с - 0,99 =99%, и что "плохое" = 93%.

ABCDA₁B₁C₁D₁ - правильная четырёхугольная призма с основаниями ABCD и A₁B₁C₁D₁ .

Основания это квадраты т.к. призма прав., так же боковые рёбра перпендикулярны основаниям. Значит боковые грани это равные прямоугольники.

D₁B = 8√2 см.

В ΔD₁DB:

∠D₁DB = 90°; ∠D₁BD = 45° т.к. DB это проекция D₁B на основание ABCD; значит ∠DD₁B = 90°-45° = 45°.

ΔD₁DB - прямоугольный и равнобедренный с гипотенузой 8√2 см, поэтому катеты DD₁ и DB равны 8√2÷√2 = 8см.

В квадрате ABCD диагональ равна 8см, значит стороны равны 8÷√2 = 4√2 см.

см².

S(бок) = 4·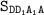 = 4·32√2 = 128√2 см².

ответ: 128√2 см².