В ящике 9 белых 4 черных шаров. Из него наудачу вынимают шар, фиксируют его цвет и возвращают шар назад в ящик. Назовем «белым пулом» любую максимальную цепочку подряд вынутых белых шаров. Найти математическое ожидание количества «белых пулов» при извлечении из ящика 10 шаров. (задание4)

Стратегия первого: для начала он разбивает 25 камешков на кучки по 1 и по 2. Так, 25=12*2+1, так что он мысленно (или непосредственно раскладывает) разбивает все камешки на 12 пар и 1 камешек. Пусть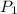 - это количество групп по одному камешку, а 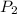- соответственно по два. Назовем разбиение хорошим, если 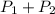нечетно. Если в некоторый момент времени 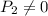, то первый всегда может менять четность суммы 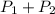, убирая один камешек из групп по одному камешку или два камешка из групп по двое и сохранять ее, убирая один камешек из групп по двое. Если 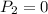и игра еще не окончена, то первый опять мысленно разбивает все камешки на группы по одному и по двое. Стратегия первого будет заключаться в том, чтобы каждый раз после его хода разбиение было хорошим, что, как мы показали, всегда возможно.

Обозначим сторону маленького квадрата за х. Тогда площадь основания коробки будет равна S=(a-2x)^2, а объем коробки будет равен V=(a-2x)^2*x=a^2*x-4*a*x^2+4*x^3. 
Для нахождения максимума объема продифференцируем эту функцию по x, получим 12*x^2-8*a*x+a^2. Приравняем производную нулю и решим полученное уравнение относительно x: 
x1,2=(8a+/-sqrt(64a^2-48a^2))/24=(8a+/-4a)/24 
x1=1/6*a 
x2=1/2*a 
Очевидно, что при x=1/2*объем коробки равен 0, и равенство производной нулю в этой точке указывает на минимум функции объема (при изменении х от 0 до 1/2*a).. 
А x=1/6*a является точкой максимума функции объема. 
ответ: сторона вырезаемого по углам квадрата должна быть равна 1/6 части стороны исходного квадрата.