а) Найдем точки пересечения указанных графиков и (рис. 1), приравняв правые части:
Так как на промежутке то применяя формулу Ньютона-Лейбница, получаем
б) Нарисуем в одной координатной плоскости все указанные линии и заштрихуем область, площадь которой необходимо найти. Разобьем получившуюся фигуру на две части прямой (рис. 2).
Тогда левая часть фигуры — квадрат со стороной 1, его площадь равна 1.
Площадь правой части фигуры найдем как площадь криволинейной трапеции, ограниченной графиком функции прямыми и используя формулу Ньютона-Лейбница:
Таким образом, площадь заданной фигуры равна 1 + 1 = 2.
в)
(рис. 3 для случая ).
Решаем неравенство
Для вычисления площади криволинейного сектора воспользуемся формулой
Из формулы синуса тройного угла следует, что
Тогда
Понижая степень синуса и записывая произведение синусов в виде суммы, получим
а)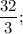 б) 2; в)
б) 2; в) 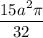
Пошаговое объяснение:
а) Найдем точки пересечения указанных графиков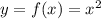 и
и 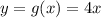 (рис. 1), приравняв правые части:
(рис. 1), приравняв правые части:
Так как на промежутке![[0;\,\,4]](/tpl/images/4978/6389/04e4e.png)
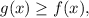 то применяя формулу Ньютона-Лейбница, получаем
то применяя формулу Ньютона-Лейбница, получаем
б) Нарисуем в одной координатной плоскости все указанные линии и заштрихуем область, площадь которой необходимо найти. Разобьем получившуюся фигуру на две части прямой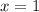 (рис. 2).
(рис. 2).
Тогда левая часть фигуры — квадрат со стороной 1, его площадь равна 1.
Площадь правой части фигуры найдем как площадь криволинейной трапеции, ограниченной графиком функции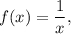 прямыми
прямыми 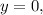
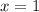 и
и 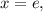 используя формулу Ньютона-Лейбница:
используя формулу Ньютона-Лейбница:
Таким образом, площадь заданной фигуры равна 1 + 1 = 2.
в)
(рис. 3 для случая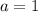 ).
).
Решаем неравенство
Для вычисления площади криволинейного сектора воспользуемся формулой
Из формулы синуса тройного угла следует, что
Тогда
Понижая степень синуса и записывая произведение синусов в виде суммы, получим
Тогда площадь