В зависимости от исходных данных. Задать граф, представленный множеством вершин и ребер, графически и

матрицами, преобразовать граф в плоский, вычислить степени его вершин. Задать граф, представленный матрицей инцидентности, алгебраически, графически и матрицей смежности, преобразовать граф в плоский, вычислить

степени его вершин.

Задать граф, представленный графически, множеством вершин и ребер и

матрицами, преобразовать граф в плоский, вычислить степени его вершин.

Пошаговое объяснение:

7. Разложим на простые множители

225 = 3 * 3 * 5 * 5

45 = 3 * 3 * 5

270 = 2 * 3 * 3 * 3 * 5

Запишем все так, чтобы не повторялись: Возьмем разложение 270

2 * 3 * 3 * 3 * 5

В этом разложении полностью содержится разложение 45. (помечено)

2 * 3 * 3 * 3 * 5

Также в этом разложении не хватает одной 5 чтобы содержалось разложение 225. Добавим ее туда

2 * 3 * 3 * 3 * 5 * 5

Тогда это и есть НОК. Считаем

2 * 3 * 3 * 3 * 5 * 5 = 1350

И это ответ!

8.  По известному тождеству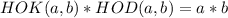 запишем НОD

И это ответ!

Пошаговое объяснение:

7. Разложим на простые множители

225 = 3 * 3 * 5 * 5

45 = 3 * 3 * 5

270 = 2 * 3 * 3 * 3 * 5

Запишем все так, чтобы не повторялись: Возьмем разложение 270

2 * 3 * 3 * 3 * 5

В этом разложении полностью содержится разложение 45. (помечено)

2 * 3 * 3 * 3 * 5

Также в этом разложении не хватает одной 5 чтобы содержалось разложение 225. Добавим ее туда

2 * 3 * 3 * 3 * 5 * 5

Тогда это и есть НОК. Считаем

2 * 3 * 3 * 3 * 5 * 5 = 1350

И это ответ!

8.  По известному тождеству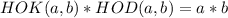 запишем НОD

И это ответ!