Ваня7/12 ч потратил на выполнение задания по математике, что на 3/20 ч больше, чем он потратил на заданне по литературе. Сколько всего времени выполнял Ваня домашнее задание по математике и литературе?
Геометрическая прогрессия это умножение. q - коэффицент.
Есть формула
По данной формуле подставим наши значения
b(2) = -1,1*2 = -2,2
b(3) = -2,2*2=-4,4 (или b(3)=-1,1*2^2=-1,1*4=-4,4)
Если у нас известен первый член геометрической прогрессии и коэффиент и надо найти какой-нибудь член под номер 10, можно прост перемножать первый член на коэффицент, если забыл формулу (10 раз)
И так, надо найти сумму
b(1)=-1,1
b(2)=-2,2
b(3)=-4,4
S(3)=-1,1+(-2,2)+(-4,4)=-7,7 (+ перед скобкой не меняет знака, сл-но - остается)
Это один из в лоб, есть формула нахождения суммы членов геометрическй прогрессии
Попробуем найти по этой формуле, ( -1,1 (2^3-1) )/ (2-1) = -7,7
Формулой удобно, но если забыл, то только в лоб, или выводить формулу)
1) Эта запись означает, что если x стремится к x0=3 справа, то есть оставаясь больше, чем 3, то значения функции f(x) при этом неограниченно приближаются к числу 7. Иными словами: сколь бы малое число ε>0 ни взять, найдётся такое положительное число δ, что для всех значений x из интервала (3; 3+δ) будет выполняться неравенство /f(x)-7/<ε (здесь чертами / / обозначен модуль).
2) Буквами sup обозначается точная верхняя граница некоторого множества. В данном случае таким множеством является множество значений функции f(x) из интервала x∈[1;2]. Это значит, что либо наибольшее значение функции f(x) на этом интервале равно 5, либо значения этой функции в одной или нескольких точках данного интервала неограниченного приближаются к числу 5, то есть предел функции f(x) в этой точке (в этих точках) равен 5. Обобщая, можно сказать так: запись sup f(x)=5 при x∈[1;2] означает, что предел функции f(x) в одной, нескольких или даже во всех точках интервала x∈[1;2] равен 5.
-7,7
Пошаговое объяснение:
Геометрическая прогрессия это умножение. q - коэффицент.
Есть формула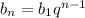
По данной формуле подставим наши значения
b(2) = -1,1*2 = -2,2
b(3) = -2,2*2=-4,4 (или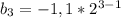
b(3)=-1,1*2^2=-1,1*4=-4,4)
Если у нас известен первый член геометрической прогрессии и коэффиент и надо найти какой-нибудь член под номер 10, можно прост перемножать первый член на коэффицент, если забыл формулу (10 раз)
И так, надо найти сумму
b(1)=-1,1
b(2)=-2,2
b(3)=-4,4
S(3)=-1,1+(-2,2)+(-4,4)=-7,7 (+ перед скобкой не меняет знака, сл-но - остается)
Это один из в лоб, есть формула нахождения суммы членов геометрическй прогрессии
Попробуем найти по этой формуле, ( -1,1 (2^3-1) )/ (2-1) = -7,7
Формулой удобно, но если забыл, то только в лоб, или выводить формулу)
Пошаговое объяснение:
1) Эта запись означает, что если x стремится к x0=3 справа, то есть оставаясь больше, чем 3, то значения функции f(x) при этом неограниченно приближаются к числу 7. Иными словами: сколь бы малое число ε>0 ни взять, найдётся такое положительное число δ, что для всех значений x из интервала (3; 3+δ) будет выполняться неравенство /f(x)-7/<ε (здесь чертами / / обозначен модуль).
2) Буквами sup обозначается точная верхняя граница некоторого множества. В данном случае таким множеством является множество значений функции f(x) из интервала x∈[1;2]. Это значит, что либо наибольшее значение функции f(x) на этом интервале равно 5, либо значения этой функции в одной или нескольких точках данного интервала неограниченного приближаются к числу 5, то есть предел функции f(x) в этой точке (в этих точках) равен 5. Обобщая, можно сказать так: запись sup f(x)=5 при x∈[1;2] означает, что предел функции f(x) в одной, нескольких или даже во всех точках интервала x∈[1;2] равен 5.