Вариант
А1. Найдите значение выражения
х−1х
, если х = 0,75
ответ:
А2. Товар стоил 2500руб. сколько стал стоить этот товар после повышения цены на 5 %?
1) 3000р. 2) 2625р. 3) 2550р. 4) 310р.
А3. Приведите подобные слагаемые в выражении 8х+7-х-11.
1) 9х 2) х-12 3) 8х+4 4) 7х-4
А4. Вычислите:
35∗9233
64 2) 9 3)
19
4)
181
А5. Разложите на множители многочлен 25х2 – 121
1) (5x – 11)2 2) 25(x2 – 121)
3) (25x – 11)(25x + 11) 4) (5x – 11)(5x + 11)
А6. Решите уравнение 2(3+х) – х = 12
ответ:
А7. Определите какая из точек не принадлежит графику функции y=3x-24
(7;-3) 2) (0;-24) 3) (-1;32) 4) (5;-9)
А8. Решите систему уравнений:
{4x−y=11,6x−2y=13.
(
29
; 2 ) 2) (-3;0) 3) (2;-1) 4) (4,5;7)
часть.
В1. ( ) Прямая y=kx+b проходит через точки А(4;0) и В(2;-5). Напишите уравнение прямой.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
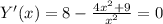
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении