Вцентре доски 101×101 стоит фишка. за один ход её можно передвинуть по горизонтали на m клеток (влево или вправо), а затем по вертикали на n клеток (вверх или вниз), или наоборот: по вертикали на m клеток, а затем по горизонтали на n клеток (например, если m=1 и n=2, то указанный ход — это ход коня). в каких случаях фишку можно за несколько ходов переместить на клетку, соседнюю с центральной? m=1,n=1 m=1, n=2 m=1,n=3 m=1, n=4 m=2,n=2 m=2, n=3 m=2,n=4 m=3,n=3 m=3, n=4

Показать ответ

Ответ:

Theyom47

31.07.2021 11:23

На Тенистой улице живут 11 учеников из школы. В школе 2 первых класса, 2 вторых класса, 2 третьих класса, 1 четвёртый класс. ответьте, есть ли среди учеников, которые живут на Тенистой улице, хотя бы двое, которые учатся у одного и того же учителя. Объясните свой ответ.

Решение

2+2+2+1=7 количество классов в школе

Минимальное количество учеников с Тенистой улицы (для возможности учебы у каждого из семи учителей) равно 7. В этом случае количество учеников может распределится среди учителей так, что каждому учителю достанется по одному ученику с Тенистой улицы. А так как на улице живут 11 учеников > 7 учеников, значит есть хотя бы двое учеников, которые учатся у одного и того же учителя

0,0(0 оценок)

Ответ:

aldynsaioorzhak1

22.03.2023 23:10

1) Получаем треугольник AOB (см.рис1), стороны которого нам известны (AO=10 см, BO = 6 см, AB = 14 см). Из этого треугольника по теореме косинусов:

$\\AB^2=AO^2+BO^2-2\cdot AO\cdot BO\cdot\cos\hat{AOB}\Rightarrow\\\cos\hat{AOB}=\frac{AO^2+BO^2-AB^2}{2\cdot AO\cdot BO}=\frac{100+36-196}{2\cdot10\cdot6}=-\frac{60}{120}=-\frac12\Rightarrow\\AOB=\frac{2\pi}3=120^0$ .

2) (см.рис2) Угол CDO - прямой, т.к. CD - расстояние от вершины С до грани угла (перпендикуляр). Значит, треугольник COD - прямоугольный, CO - гипотенуза. В то же время CO - высота равностороннего треугольника ABC.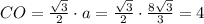 $\\CO=\frac{\sqrt3}2\cdot a=\frac{\sqrt3}2\cdot\frac{8\sqrt3}3=4$

Из треугольника COD по определению синуса, синус угла COD равен отношению противолежащего катета CD к гипотенузе CO sinO= 2/4 = 1/2. То есть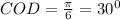 $COD=\frac{\pi}6=30^0$

3) (см.рис3) В треугольнике EOF сторона EO - это высота равностороннего трегольника ABE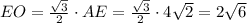 $EO=\frac{\sqrt3}2\cdot AE=\frac{\sqrt3}2\cdot4\sqrt2=2\sqrt6$

Сторона OF равна стороне квадрата, DF равна половине стороны квадрата (OF - средняя линия ABCD), сторону EF найдём из прямоугольного треугольника EFD (EF перпендикуляр к CD => EFD - прямоугольный, ED - гипотенуза):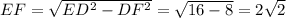 $EF=\sqrt{ED^2-DF^2}=\sqrt{16-8}=2\sqrt2$ .

Тогда из треугольника EOF по тереме косинусов:

$\\EF^2=OE^2+OF^2-2\cdot OE\cdot OF\cdot\cos\hat{EOF}\Rightarrow\\\cos\hat{EOF}=\frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF}=\frac{24+32-8}{2\cdot2\sqrt6\cdot4\sqrt2}=\frac{48}{16\sqrt{12}}=\frac{48}{32\sqrt3}=\frac{3}{2\sqrt3}=\frac{\sqrt3}2\\\Rightarrow \hat{EOF} = \frac{\pi}6=30^0$