Пускай сейчас сыну x лет, тогда отцу — 5x. Пять лет назад им было (x-5) и (5x-5) лет соответственно. Факт того, что на тот момент возраст отца был в 10 раз больше возраста сына, можно записать в виде уравнения:
10(x-5) = 5x-5 (то есть если бы сын был в десять раз старше, его возраст сравнился бы с возрастом отца). Решим это уравнение:
10x-50 = 5x-5
10x-5x = 50-5
5x = 45
x = 9
Получили, что сыну сейчас 9 лет, тогда отцу — 9·5 = 45, а разница между их возрастами составляет 45-9 = 36 лет.
Касательные — это прямые вида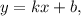
где 
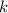и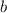 
— некоторые числа.
Если прямые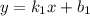
и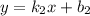 
параллельны, то 
За коэффициент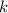
касательной отвечает производная 
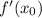функции в точке с абсциссой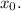 
1. Найдем производную функции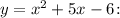
2. Определим абсциссу точки касания.
2.1. Для прямой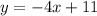
коэффициент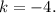 
2.2. Для функции
касательная в данной точке по геометрическому смыслу производной имеет угловой коэффициент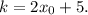 
2.3. Поскольку прямая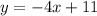
параллельна касательной к графику функции 
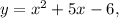то:
Таким образом,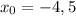
— абсцисса точки касания к графику функции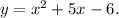 
ответ: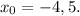
36 лет
Пошаговое объяснение:
Пускай сейчас сыну x лет, тогда отцу — 5x. Пять лет назад им было (x-5) и (5x-5) лет соответственно. Факт того, что на тот момент возраст отца был в 10 раз больше возраста сына, можно записать в виде уравнения:
10(x-5) = 5x-5 (то есть если бы сын был в десять раз старше, его возраст сравнился бы с возрастом отца). Решим это уравнение:
10x-50 = 5x-5
10x-5x = 50-5
5x = 45
x = 9
Получили, что сыну сейчас 9 лет, тогда отцу — 9·5 = 45, а разница между их возрастами составляет 45-9 = 36 лет.