Вдесятичной записи 13 натуральных чисел используется одна и аде цифра n и не используются другие цифры. может ли сумма всех этих 13 чисел равняться 8900098?
1)И так, сначала находим 1%: 1) 8400кг:100=84кг, и умножаем его на 45 2)84кг*45= 3780кг, ответ: 3780кг антоновских яблок собрали в саду. Вторая задача) переводим тонны в кг= 25,5*1000=25500кг, находим 1% 1)25500кг:100=255кг, и умножаем его на 40 : 2)255кг*40=10200кг,ответ:10200кг муки получилось из овса. третья задача) находим 1% делим на 65, потому, что 325 это лишь 65 % поля: 325:65=5га, получается 1%=5га, ну а чтобы получить 100%нужно умножить 1% на 100 5га*100=500гаответ: Площадь всего поля 500га.
Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
; Сперва очевидно, что делится на 9. Согласно малой теореме Ферма , так как 1987 - число простое. Так как 9 и 1987 взаимно просты, то число XX...X делится на 1987 для n+1=1986, т.е. для n=1985.
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как , где каждое из чисел вида X...X делится на 1987
1)И так, сначала находим 1%: 1) 8400кг:100=84кг, и умножаем его на 45 2)84кг*45= 3780кг, ответ: 3780кг антоновских яблок собрали в саду. Вторая задача) переводим тонны в кг= 25,5*1000=25500кг, находим 1% 1)25500кг:100=255кг, и умножаем его на 40 : 2)255кг*40=10200кг,ответ:10200кг муки получилось из овса. третья задача) находим 1% делим на 65, потому, что 325 это лишь 65 % поля: 325:65=5га, получается 1%=5га, ну а чтобы получить 100%нужно умножить 1% на 100 5га*100=500гаответ: Площадь всего поля 500га.
Лемма: существует такое y-значное число вида XX...X (т.е. состоит из целиком из цифр X) такое, что оно делится на число 1987
Доказательство: число указанного вида можно представить в виде
Итак, взяв например n=1985 получим число 1...19...98...86...6, которое раскладывается как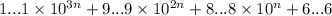
, где каждое из чисел вида X...X делится на 1987