ВЕКТОРНА АЛГЕБРА Задані координати вершин піраміди M1M2M3M4 . Для всіх варіантів виконати наступні завдання. Завдання 2.1. Знайти кут між ребрами M1M2 та M1M4 . Завдання 2.2. Знайти проекцію вектора M1M3 на вектор M1M4 . Завдання 2.3. Знайти площу грані M1M2M3 . Завдання 2.4. Знайти довжину висоти піраміди, проведену з вершини M4 , попередньо знайшовши об"єм піраміди. Завдання 2.5. Встановити орієнтацію трійки векторів M1M2 , M1M3 і M1M4
Правильная четырехугольная пирамида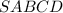 .
.
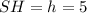 (см).
(см).
Найти: - сторону основания.
- сторону основания.
Решение:Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
Попробуем выразить через
через  (сторону основания) и
(сторону основания) и 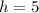 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный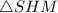 (где
(где 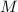 - середина
- середина 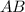 ). В нем
). В нем 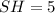 (см), а
(см), а 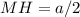 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
- неотрицательное):
Пусть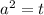 :
:
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
ответ:Пошаговое объяснение:
формулы:
M[X] = ∑xₐpₐ
D[X] = ∑xₐ²pₐ - M²[X]
δ(x) = √D[X[
а)
хₐ 0 1 2 3
рₐ 0,68 0,283 0,032 0,001
M[x] = 0*0.684 + 1*0.283 + 2*0.032 + 3*0.001 = 0.35
D[X] = 0²*0.684 + 1²*0.283 + 2²*0.032 + 3²*0.001 - 0.35² = 0.298
δ(x) = √(0.298)
б)
хₐ 1 4 9
рₐ 0,3 0,4 0,3
M[x] = 4,6
D[X] = 9,84
δ(x) = √(9,84)
в)
хₐ -5 2 3 4
рₐ 0,4 0,3 0,1 0,2
M[x] = -0,3
D[X] = 15,21
δ(x) = √(15,21)
г)
хₐ 25 4 9 16
рₐ 0,4 0,3 0,1 0,2
M[x] = 15,3
D[X] = 80,01
δ(x) = √(80,01)