Геометрический смысл производной: производная функции в точке x0 есть тангенс угла наклона касательной к этой функции, проведенной в точке x0. Угол наклона считают против часовой стрелки от положительного направления оси абсцисс, который мы обозначим за
где - угол смежный с .
Жирные точки на прямой поставлены для удобного вычисления тангенса угла бета. Его легко можно посчитать, если опустить вертикальную линию вниз из левой жирной точки, а из правой жирной точки горизонтальную линию. Тогда эти две точки и точка пересечения проведенных линий образуют прямоугольный треугольник с катетами 3 и 6. Тангенс угла определяется как отношение катета, противолежащего углу, к прилежащему катету: . Таким образом,
так как нам известна разность, найдём произведение, для этого это выражение возведем в квадрат (sin-cos)²=(0,3)² (альфа везде сам/а допишешь, чтоб не запутались
sin²-2sin*cos²=0,09
1-2sin*cos=0,09
-2sin*cos=0.09-1
sin*cos=0,455
2) sin₄+cos₄ - это та же формула сокращенного умножения, который не хватает +2sin²*cos², но если мы что-то добавляем, то это же число или выражение мы отнимаем, значит
sin₄+cos₄+2sin²cos²-2sin²cos²=(sin²+cos²)²-2sin²*cos²=1-2sin²cos² (а произведением нам известно, просто подставляем) = 1-2*0,455=1-0,91=0,09
Всё, что и требовалось решить, если нужно было найти разность их, то квадратных скобках был бы минус, а выносили бы +2sin²cos²
-0.5
Пошаговое объяснение:
Геометрический смысл производной: производная функции в точке x0 есть тангенс угла наклона касательной к этой функции, проведенной в точке x0. Угол наклона считают против часовой стрелки от положительного направления оси абсцисс, который мы обозначим за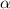
Жирные точки на прямой поставлены для удобного вычисления тангенса угла бета. Его легко можно посчитать, если опустить вертикальную линию вниз из левой жирной точки, а из правой жирной точки горизонтальную линию. Тогда эти две точки и точка пересечения проведенных линий образуют прямоугольный треугольник с катетами 3 и 6. Тангенс угла определяется как отношение катета, противолежащего углу, к прилежащему катету: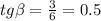 . Таким образом,
. Таким образом,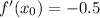
По шагам решать буду
Пошаговое объяснение:
так как нам известна разность, найдём произведение, для этого это выражение возведем в квадрат (sin-cos)²=(0,3)² (альфа везде сам/а допишешь, чтоб не запуталисьsin²-2sin*cos²=0,09
1-2sin*cos=0,09
-2sin*cos=0.09-1
sin*cos=0,455
2) sin₄+cos₄ - это та же формула сокращенного умножения, который не хватает +2sin²*cos², но если мы что-то добавляем, то это же число или выражение мы отнимаем, значит
sin₄+cos₄+2sin²cos²-2sin²cos²=(sin²+cos²)²-2sin²*cos²=1-2sin²cos² (а произведением нам известно, просто подставляем) = 1-2*0,455=1-0,91=0,09
Всё, что и требовалось решить, если нужно было найти разность их, то квадратных скобках был бы минус, а выносили бы +2sin²cos²