Выполним еще одну замену: z(x)=u(x)*v(x), вычислим
+
(du/dx)*v+u(dv/dx-v)=x (1) - таким стало уравнение после соответствующих подстановок.
Теперь выбираем функцию v(x), так чтобы v'-v=0, чтобы обнулить слагаемое
u(dv/dx-v) в уравнении (1). Решив это уравнение, оно элементарное с разделяющимися переменными, получим Подставляем вычисленное v(x) в уравнение (1) и получаем:
, решаем его методом разделения переменных и получаем
u(x)= +C, где C-константа.
Возвращаемся к выражению z(x)=u(x)v(x)=*( +C )=-x-1+C*e^x.
Т.е.
y'(x)=-x-1+C* .
Решаем это уравнение получаем dy=( -x-1+C* )dx
Получаем y(x)= +C1, где С и С1 это константы которые находятся из начальных условий.
Сделаем замену y'=z(x), получим уравнение z'=z+x.
Выполним еще одну замену: z(x)=u(x)*v(x), вычислим
(du/dx)*v+u(dv/dx-v)=x (1) - таким стало уравнение после соответствующих подстановок.
Теперь выбираем функцию v(x), так чтобы v'-v=0, чтобы обнулить слагаемое
u(dv/dx-v) в уравнении (1). Решив это уравнение, оно элементарное с разделяющимися переменными, получим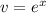
Подставляем вычисленное v(x) в уравнение (1) и получаем:
u(x)=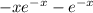
+C, где C-константа.
Возвращаемся к выражению z(x)=u(x)v(x)=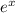
*( 
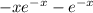+C )=-x-1+C*e^x.
Т.е.
y'(x)=-x-1+C*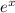
.
Решаем это уравнение получаем dy=( -x-1+C*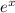
)dx
Получаем y(x)=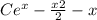
+C1, где С и С1 это константы которые находятся из начальных условий.
ответ: y(x)=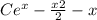
+C1, где С и С1- const
у=(х-5)²·(х-3)+ 10
y' = 2·(х-5)·(х-3) + (х-5)²
ищем минимум
2·(х-5)·(х-3) + (х-5)² = 0
(х-5)·(2х - 6 + х - 5) = 0
(х-5)·(3х - 11) = 0
х₁ = 5, х₂ = 11/3 = 3 2/3
Исследуем знак производной в интервалах
+ - +
11/3 5
У'(3) = -2·(-2) = 4 > 0 y возрастает
У'(4) = -1·1 = -1 < 0 y убывает
У'(6) = 1·7 = 7 > 0 y возрастает
Точка минимума х₁ = 5
У min = у(5) = (5-5)²·(5-3)+ 10 = 0·2 + 10 = 10
На промежутке от 4 до 8 функция ведёт себя так:убывает при х∈[4 ; 5] и возрастает при ∈[5 ; 8].
Следовательно, наименьшее значение функции совпадает с её минимальным значением
ответ: у наим = 10