Дано:
Δ ABC
BH - высота = 4 см
∠BAH = 30°
∠BCH = 45°
Найти: S Δ ABС
Решение: 1) S Δ ABС = 1/2 * AC * BH
2) Рассмотрим ΔBCH
Т.к. BH - высота ⇒ ΔBCH - прямоугольный
∠CBH = 90° - ∠BCH = 90° - 45° = 45°
∠CBH = ∠BCH = 45° ⇒ ΔBCH - равнобедренный ⇒ BH = CH = 4 см
3)Рассмотрим ΔBAH
Напротив угла в 30° лежит сторона = половине гипотенузы ⇒ 2BH = BA
BA = 2*4 = 8
По т.Пифагора
AH =
4) AC = AH + CH = 4√3 + 4 = 8√3
5)S Δ ABС = 1/2 * 8√3 * 4 = 4√3 * 4 = 16√3
ответ: S Δ ABС = 16√3
Дано:
Δ ABC
BH - высота = 4 см
∠BAH = 30°
∠BCH = 45°
Найти: S Δ ABС
Решение: 1) S Δ ABС = 1/2 * AC * BH
2) Рассмотрим ΔBCH
Т.к. BH - высота ⇒ ΔBCH - прямоугольный
∠CBH = 90° - ∠BCH = 90° - 45° = 45°
∠CBH = ∠BCH = 45° ⇒ ΔBCH - равнобедренный ⇒ BH = CH = 4 см
3)Рассмотрим ΔBAH
Т.к. BH - высота ⇒ ΔBCH - прямоугольный
Напротив угла в 30° лежит сторона = половине гипотенузы ⇒ 2BH = BA
BA = 2*4 = 8
По т.Пифагора
AH =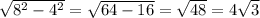
4) AC = AH + CH = 4√3 + 4 = 8√3
5)S Δ ABС = 1/2 * 8√3 * 4 = 4√3 * 4 = 16√3
ответ: S Δ ABС = 16√3