111/11
Пошаговое объяснение:
запишем числа в виде суммы разрядных слагаемых
ab=10a+b
ba=10b+a
aba=100a+10b+a=101a+10b
bab=101b+10a
запишем суммы
aba+bab=101a+10b+101b+10a=111a+111b=111(a+b)
ab+ba =10a+b+10b+a=11(a+b)
находим отношение
111(a+b)/11(a+b)=111/11
Сумма трёхзначных чисел равна
Сумма двузначных чисел равна
Найдём, во сколько раз сумма трёхзначных чисел больше суммы двузначных чисел .
ответ: в раз .
111/11
Пошаговое объяснение:
запишем числа в виде суммы разрядных слагаемых
ab=10a+b
ba=10b+a
aba=100a+10b+a=101a+10b
bab=101b+10a
запишем суммы
aba+bab=101a+10b+101b+10a=111a+111b=111(a+b)
ab+ba =10a+b+10b+a=11(a+b)
находим отношение
111(a+b)/11(a+b)=111/11
Сумма трёхзначных чисел равна
Сумма двузначных чисел равна
Найдём, во сколько раз сумма трёхзначных чисел больше суммы двузначных чисел .
ответ: в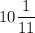 раз .
раз .