поскольку все прямые пересекаются в одной точке (хₙ; уₙ), для всех координаты этой точки пересечения будут (хₙ; 3), т.к. последняя прямая - это линия параллельная оси ох и координата уₙ =3
тогда просто найдем зависимость m от t
из уравнения первой прямой
mx+1 = 3 ⇒ x= 2/m
подставим этот х в уравнение второй прямой
x+t =3 2/m = 3-t ⇒
вот при всех таких m, вычисляемых в зависимости от t, при t≠ 3, прямые и будут пересекаться в одной точке
Пошаговое объяснение:
y₁=mx+1
y₂ = x+t
y₃ = 3
поскольку все прямые пересекаются в одной точке (хₙ; уₙ), для всех координаты этой точки пересечения будут (хₙ; 3), т.к. последняя прямая - это линия параллельная оси ох и координата уₙ =3
тогда просто найдем зависимость m от t
из уравнения первой прямой
mx+1 = 3 ⇒ x= 2/m
подставим этот х в уравнение второй прямой
x+t =3 2/m = 3-t ⇒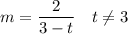
вот при всех таких m, вычисляемых в зависимости от t, при t≠ 3, прямые и будут пересекаться в одной точке
x ∈ (-1; 3)
Пошаговое объяснение:
|x² - 2x - 3| > x² - 2x - 3 <=> (это неравенство равносильно следующей системе неравенств)
{x² - 2x - 3 > x² - 2x - 3 при x ∈ (-∞; -1] ∪ [3; +∞),
{-(x² - 2x - 3) > x² - 2x - 3 при x ∈ (-1; 3)
{x ∈ ∅ (потому что выходит, что 0 > 0 - это неверно),
{-x² + 2x + 3 - x² + 2x + 3 > 0, при x ∈ (-1; 3)
Решаем второе неравенство:
-2x² + 4x + 6 > 0, при x ∈ (-1; 3)
Корни по т-ме Виета: -1, 3, поэтому:
-(x + 1)(x - 3) > 0, при x ∈ (-1; 3)
- + -
оо>
-1 3 x
ответ: x ∈ (-1; 3)