Вправильной четырёхугольной пирамиде sabcd ( s – вершина) sa=2ab . перпендикуляр, опущенный из точки b на ребро sd , пересекает его в точке k . на апофеме sf грани sab взята точка m так, что sm: sf=4: 5 . сфера с центром на прямой mk , проходит через точки b , k и пересекает прямую ab в точке p , причём bp=d . найдите длину отрезка ab .
Из условия следует, что ни у кого нет троих не знакомых с ним, а также то, что нет тройки попарно незнакомых. В противном случае к ним добавляем каких-то двоих, и этих пятерых будет не рассадить.
Из условия следует, что ни у кого нет троих не знакомых с ним, а также то, что нет тройки попарно незнакомых. В противном случае к ним добавляем каких-то двоих, и этих пятерых будет не рассадить.Рассмотрим дополнение графа знакомств в полном графе -- это удобно, так как рёбер мало. Степень каждой вершины не больше 2, и в графе нет треугольников. Рассмотрим связную компоненту. Это или линейный граф (возможно, из одной вершины), или цикл. Будем в каждой компоненте выбирать подмножество вершин, в котором нет соединений. Если мы в сумме наберём 12 человек, то задача решена: представители разных компонент между собой знакомы.
Из условия следует, что ни у кого нет троих не знакомых с ним, а также то, что нет тройки попарно незнакомых. В противном случае к ним добавляем каких-то двоих, и этих пятерых будет не рассадить.Рассмотрим дополнение графа знакомств в полном графе -- это удобно, так как рёбер мало. Степень каждой вершины не больше 2, и в графе нет треугольников. Рассмотрим связную компоненту. Это или линейный граф (возможно, из одной вершины), или цикл. Будем в каждой компоненте выбирать подмножество вершин, в котором нет соединений. Если мы в сумме наберём 12 человек, то задача решена: представители разных компонент между собой знакомы.Для линейного графа раскрасим вершины через одну, и возьмём тот цвет, представителей которого не меньше. Это даст как минимум половину. Если цикл имеет чётную длину, то мы также выбираем половину -- через одного. Наконец, пусть цикл имеет длину 2k+1, где k>=2. Тогда можно взять k человек с номерами 2, 4, ... , 2k. Доля числа взятых равна k/(2k+1)>=2/5. Отсюда следует, что мы можем взять как минимум 2/5 от общего числа, а это и есть 12. Они попарно знакомы.
Пошаговое объяснение:
а) разделил на 2 интеграла по разности, под первым e^(pi) - константа, поэтому получится e^(pi) * x = pi* e^(pi) - 0 ( при подстановке)
второй - табличный = sinx + C = 0 в подстановке.
ответ: pi* e^(pi)
б) занесу cosx под дифференциал
cosxdx = d ( sinx + 1)
дальше простой степенной интеграл = 1/3*(1+sinx)^3 + C = 1/3 * (1)^3 - 1/3 * (1)^3 = 0
в) опять под дифференциал
d(4-t^2) = -2*t dt => tdt = -1/2 * d(4-t^2)
дальше простой степенной интеграл = -1/2*2*(4-t)^(1/2) + C = -3^(1/2) + 4^(1/2) = 2 -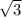
г) под дифференциал:
d(1 + 4x^3) = 12x^2 dx => 6x^2dx = 1/2 d(1+4x^3)
дальше табличный интеграл = 1/2 * ln(1+4x^3) + C = 1/2*ln5 - 1/2*ln1 = 1/2*ln5