Проекция AO бокового ребра L =SA на основание равна (2/3)h, где h - высота основания.
AO = (2/3)*(6√3/2) = 2√3.
Находим высоту пирамиды Н = √(L² - AO²) = √(39 - 12) = √27 = 3√3.
Площадь основания So = a²√3/4 = (36√3)/4 = 9√3.
Объём пирамиды V = (1/3)SoH = (1/3)*(9√3)*(3√3) = 27 куб.ед.
Имеем .
В основании лежит правильный треугольник, значит площадь его .
Радиус описанной окружности равен .
Найдём по теорема Пифагора высоту:
.
Откуда площадь:
Проекция AO бокового ребра L =SA на основание равна (2/3)h, где h - высота основания.
AO = (2/3)*(6√3/2) = 2√3.
Находим высоту пирамиды Н = √(L² - AO²) = √(39 - 12) = √27 = 3√3.
Площадь основания So = a²√3/4 = (36√3)/4 = 9√3.
Объём пирамиды V = (1/3)SoH = (1/3)*(9√3)*(3√3) = 27 куб.ед.
Имеем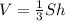 .
.
В основании лежит правильный треугольник, значит площадь его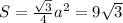 .
.
Радиус описанной окружности равен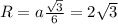 .
.
Найдём по теорема Пифагора высоту:
Откуда площадь: