Всем привет с заданием дописать пропущенное:
1.Заранее заданное число , которое нельзя менять в процессе сужения интервала , и если после N испытаний не получена нужная определения оптимума, то все приходится начинать , задавшись большим N..
2.При применении ЭВМ необходимо (или каждый раз вычислять) числа .
ответ: а) 4/91, б) 0, в) 53/65
Пошаговое объяснение:
а) Будем извлекать по одному фрукту. Вероятность того, что первым вынуто яблоко
Р₁ = 6/(6 + 9) = 2/5. Вероятность того, что вторым извлечено яблоко
Р₂ = 5/(5 + 9) = 5/14. Третьим — Р₃ = 4/(4+9) = 4/13. Полную вероятность найдём по формуле умножения вероятностей: Р = Р₁·Р₂·Р₃ = 2·5·4/(5·14·13) = 4/91 ≈ 0,044
б) В данном случае нужно найти вероятность того, что извлекли 2 фрукта. Но известно, что извлекли 3 фрукта. События несовместны, вероятность Р = 0
в) Найдём вероятность того, что не извлечено ни одного яблока. По аналогии с задачей в пункте а), полная вероятность ¬Р равна:
¬Р = 9·8·7/(15·14·13) = 36/(15·13) = 12/65
Тогда вероятность того, что достали хотя бы одно яблоко Р равна:
Р = 1 − ¬P = 53/65 ≈ 0,815
ответ: а) 4/91, б) 0, в) 53/65
Площадь маленького прямоугольника внутри большого прямоугольника равна 15 м².
Пошаговое объяснение:
Надо найти площадь маленького (оранжевого) прямоугольника внутри большого.
Вспомним формулу площади прямоугольника:
Обозначим ширину искомого прямоугольника №3 - а м, высоту - b м
⇒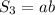
Тогда ширина прямоугольника №1 - (7-а) м,
а прямоугольника №2 - (8-а) м.
Высоты этих прямоугольников равны - b м.
А площади этих прямоугольников будут соответственно равны:
Для того, чтобы найти искомую площадь, надо найти ширину и высоту прямоугольника №3.
1. Выразим b из площади прямоугольника №1:
Подставим значение площади S₁ = 20 м² в полученное выражение:
2. Выразим b из площади прямоугольника №2:
Подставим значение площади S₂ = 25 м² в полученное выражение:
3. Приравняем выражения (1) и (2) и найдем а.
Воспользуемся основным свойством пропорции:
Произведение крайних членов равно произведению средних членов.
Раскроем скобки. Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный и решим уравнение:
⇒ ширина маленького прямоугольника равна 3 м.
4. Подставим значение а=3 в (1) или (2) равенства и найдем b.
Подставим в (1):
⇒ высота маленького прямоугольника равна 5 м.
5. Теперь, зная ширину и высоту, можем найти площадь маленького прямоугольника №3:
⇒ Площадь маленького прямоугольника равна 15 м².