Втреугольнике авс высоты, проведённые к сторонам ас, вс и вс соответственно равны 15,35 и 21 найдите: 1) площадь треугольника 2)сторону ав 3)сторону вс 4)сторону ас 5)радиус описанной окружности 6)радиус вписанной окружности 7)медиану, проведённую к стороне вс 8)биссектрису, проведённую из вершины в
Дано:
В треугольнике АВС высоты, проведённые к сторонам АС, ВС и АВ соответственно равны hb=15,ha=35 и hc=21.
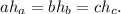
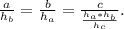
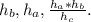
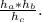равно 15*35/21 = 25.
Найти: 1) площадь треугольника
2) сторону АВ
3) сторону ВС
4) сторону АС
5) радиус описанной окружности
6) радиус вписанной окружности
7) медиану, проведённую к стороне ВС
8) биссектрису, проведённую из вершины В.
Используем равенства:
Отсюда выводим пропорции
То есть, искомый треугольник со сторонами a, b, c подобен треугольнику ВА1С1 со сторонами
Значение
Для треугольника ВА1С1 найдём высоту из вершины В.
Для этого найдём площадь ВА1С1 по Герону:
полупериметр р = (15+35+25)/2 = 75/2 = 37,5.
S(BA1C1) = √(37,5*2,5*22,5*12,5) = √26367,1875 ≈ 162,3797632.
Тогда высота в этом треугольнике из вершины В равна:
h'(B) = (2S(BA1C1))/(h(A1C1)) = (2*162,3797632)/35 = 9,278844.
Отсюда находим коэффициент пропорциональности:
к = 15/9,278844 = 1,616581.
Теперь находим искомые длины сторон:
2) сторона АВ (c) = 1,616581*25 = 40,41452,
3) сторона BС (a) = 1,616581*15 = 24,24871,
4) сторона AС (b) = 1,616581*35 = 56,58033,
1) площадь треугольника АВС = (1/2)АС*hb =
= (1/2)*56,58033*15 = 424,35245 кв.ед.
5) радиус описанной окружности R = (abc)/(4S) = 32,66667.
6) радиус вписанной окружности r = S/p = 424,35245/60,62178 = 7.
7) медиану, проведённую к стороне ВС :
ma = (1/2)√(2b²+2c²-a²) = 47,64802.
8) биссектрису, проведённую из вершины В:
βb = (2/(a+c))*√(acp(p-b)) = 15,1554.