Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение . Таким образом, синус от 60 градусов равен .
По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
sin (60°) = sin (π/3) = (√3)/2.
Пошаговое объяснение:
Синус — одна из тригонометрических функций, обозначется sin.
В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный)
Также значение синуса 60 градусов можно узнать по тригонометрической окружности (или кругу, как его еще называют).
Все значения синуса на тригонометрической окружности расположены на оси ординат. Вычислим значение синуса от 60 градусов.
Найдем на окружности значение аргумента синуса — 60 градусов. Далее опустим перпендикуляр на ось ординат и получим значение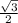
. Таким образом, синус от 60 градусов равен 
.
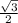По графику синуса (синусоиде) также можно найти значение синуса 60 градусов. Но для этого иметь хотя бы поверхностные знания о расположении основных значений углов и значений функции синус на координатных осях.
просто посмотреть значение в таблице.
Даны вершины треугольника АВС: А ( 1;6) В (-6;-4) С (-10;-1).
1) уравнение стороны АВ. Вектор АВ = (-6-1; -4-6) = (-7; -10).
Уравнение: (x - 1)/(-7) = (y - 6)/(-10) или 10x - 7y + 32 = 0 в общем виде.
2) уравнение высоты СН.
У перпендикуляра к прямой в виде Ax + By + C = 0 коэффициенты А и В меняются на -В и А.
СН это перпендикуляр к стороне АВ.
Уравнение СН: 7x + 10y + С = 0. Для определения слагаемого С подставим координаты точки С(-10; -1).
7*(-10) + 10*(-1) + С = 0, отсюда С = 70 + 10 = 80.
Получаем 7x + 10y + 80 = 0
3) уравнение медианы АМ.
Находим координаты точки М как середины стороны ВС.
М = (В (-6;-4) + С (-10;-1))/2 = (-8; -2,5). Точка А ( 1; 6).
Вектор АМ = (-8-1; -2,5-6) = (-9; -8,5).
Уравнение АМ: (x - 1)/(-9) = (y - 6)/(-8.5).
Или в общем виде 17x - 18y + 91 = 0.
4) точку N пересечения медианы АМ и высоты СН
.Решаем как решение системы уравнений этих прямых:
{17x - 18y + 91 = 0| x7 = 119x - 126y + 637 = 0.
{7x + 10y + 80 = 0| x(-17) = -119x - 170y - 1360 = 0.
-296y - 723 = 0,
y = -723/296 ≈ -2,442568, x = (-80 -10*-2,442568)/7 ≈ -7,93919.
5)уравнение прямой проходящей через вершину С параллельно стороне АВ.
С || АВ: 10 x - 7 y + 93 = 0.
Коэффициенты А и В сохраняются, для определения слагаемого С подставляются координаты точки С.
6) расстояние от точки С до прямой АВ
CC₂ = 2S/АВ = 4,9973147.
Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 30,5.
Расчет длин сторон:
АВ (с) = √((Хв-Ха)²+(Ув-Уа)²) = √149 ≈ 12,2066.