Вычисли объём прямоугольного параллелепипеда, стороны основания которого равны a и g, а высота равна h, если a=6см; g=6см; h=5см. Oбъём прямоугольного параллелепипеда V= см3.
Пусть Настя смогла это сделать. Разделим числа на две группы -- те, которые делятся на , но не делятся на , и те, что делятся на . Заметим, что в обеих группах поровну чисел, а потому они должны чередоваться на окружности. Поделим все числа на -- получатся числа . Теперь рядом стоящие числа взаимно просты, а четные и нечетные чередуются. Тогда рядом с числом должны располагаться два числа из (оставшиеся два нечетных делятся на ), рядом с тоже должны располагаться два из этих числа. Теперь можно попробовать расставить числа. Оказывается это возможно. Остается все умножить обратно на и записать результат: (крайние тоже соседи).
Пусть Настя смогла это сделать. Разделим числа на две группы -- те, которые делятся на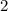 , но не делятся на
, но не делятся на  , и те, что делятся на
, и те, что делятся на  . Заметим, что в обеих группах поровну чисел, а потому они должны чередоваться на окружности. Поделим все числа на
. Заметим, что в обеих группах поровну чисел, а потому они должны чередоваться на окружности. Поделим все числа на 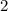 -- получатся числа
-- получатся числа 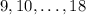 . Теперь рядом стоящие числа взаимно просты, а четные и нечетные чередуются. Тогда рядом с числом
. Теперь рядом стоящие числа взаимно просты, а четные и нечетные чередуются. Тогда рядом с числом 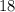 должны располагаться два числа из
должны располагаться два числа из 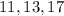 (оставшиеся два нечетных делятся на
(оставшиеся два нечетных делятся на 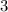 ), рядом с
), рядом с 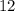 тоже должны располагаться два из этих числа. Теперь можно попробовать расставить числа. Оказывается это возможно. Остается все умножить обратно на
тоже должны располагаться два из этих числа. Теперь можно попробовать расставить числа. Оказывается это возможно. Остается все умножить обратно на 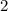 и записать результат:
и записать результат: 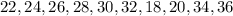 (крайние тоже соседи).
(крайние тоже соседи).
1). 15/16 > 14/15.
2). 14/17 > 10/13
Пошаговое объяснение:
1). 15/16 и 14/15
так не сравнишь, не видно. Надо привести к общему знаменателю.
16=2*2*2*2; 15=3*5 - общих множителей нет, поэтому НОК (15, 16)=3*5*8=240.
15/16=15*3*5/(240)=225/240,
14/15=14*2*2*2*2/(240)=224/240;
Теперь, когда знаменатели одинаковые, мы можем сказать, что та дробь больше, у которой больше числитель. Т.е. 225/240 > 224/240
или:
15/16 > 14/15.
2. 10/13 и 14/17
опять не видно сразу. Если делать, как в первом примере, то НОК(13, 17)=13*17 (т.к. 13 и 17 - простые числа). Умножать 13 на 17 "в уме" тяжело.
Поэтому пойдем другим путем. Сделаем равными числители дробей:
10=2*5, 14=2*7.
НОК(10, 14)=2*5*7=70
10/13=10*7/(13*7)=70/91;
14/17=5*14/(5*17)=70/85.
Вот.
Получили дроби с одинаковыми числителями, но разными знаменателями. Из этих дробей больше та, у которой меньше знаменатель.
70/85 > 70/91
или:
14/17 > 10/13