Так как цифры в записи могу повторяться, то на всех трех местах можно использовать по 3 цифры из заданных, т.е. таких
То есть, всего 27 трехзначных чисел.
Вопрос: Сколько среди них четных чисел?
Фиксируем одну цифру - четную на последнее место (ведь число четное тогда, когда последняя цифра четная). Например, зафиксируем 2, тогда на первые двух местах можно выбрать по 2 цифры,т.е. таких чисел: 2*2*1 = 4, аналогично, фиксируем на последнее место число 8, тогда таких чисел: 2*2*1 = 4. По правилу сложения, четных трехзначных чисел: 4+4=8
От пристани одновременно в противоположных направлениях отплыли две лодки.Одна лодка шла со скоростью 2 (километров/час), а скорость другой 1 (километр/час). Какое расстояние будет между лодками через 2 (часа)?
Так как цифры в записи могу повторяться, то на всех трех местах можно использовать по 3 цифры из заданных, т.е. таких
То есть, всего 27 трехзначных чисел.
Вопрос: Сколько среди них четных чисел?
Фиксируем одну цифру - четную на последнее место (ведь число четное тогда, когда последняя цифра четная). Например, зафиксируем 2, тогда на первые двух местах можно выбрать по 2 цифры,т.е. таких чисел: 2*2*1 = 4, аналогично, фиксируем на последнее место число 8, тогда таких чисел: 2*2*1 = 4. По правилу сложения, четных трехзначных чисел: 4+4=8
Нечетных трехзначных чисел всего: 27 - 8 = 19.
Самое маленькое трехзначное число: 238
Самое большое трехзначное число: 832.
От пристани одновременно в противоположных направлениях отплыли две лодки.Одна лодка шла со скоростью 2 (километров/час), а скорость другой 1 (километр/час). Какое расстояние будет между лодками через 2 (часа)?
Краткая запись:V₁ (первой лодки) =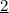
(километра/час);
V₂ (второй лодки) =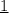
(километр/час);
S (через 2 (часа) ) =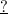
(километров).
Решение:Формула скорости удаления:
;
Формула пути (расстояния):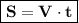
;
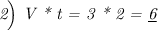(километров) путь между лодками через 2 (часа).
ответ: 6 (километров) расстояние между лодками.