Имеем несобственный интеграл 1-го рода:
По формуле: имеем:
Как видно из результата - интеграл сходится.
Имеем несобственный интеграл 1-го рода:
По формуле: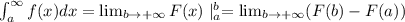 имеем:
имеем:
Как видно из результата - интеграл сходится.