Вектор нормали найдём из векторного произведения векторов a и M₁M₂
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему:
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Воспользуемся тем что число делится на 9 , тогда и только тогда когда сумма его цифр делится на 9 . Из первого члена очевидно что оно делится на 9 , так как степень 3 запишем ее в виде то есть второй член тогда будет равен заметим то что каждый член будет делится на 9 , потому сумма каждого числа делится на 9. То есть кратно Возьмем для начало такое число то есть пусть она по количеству цифр будет равна количеству цифр числа , очевидно что это число будет иметь по крайней мере цифр то есть мы предположим что самое максимальное число заданными только 9 и их сумма уже будет равна 9*1000=9000, но возьмем еще 8 , для того что бы посмотреть максимальную сумму , 9*1008=9072 то есть видно что второе число уже будет грубо , и , , , и.т.д и очевидно ответ 9
1.
Уравнение плоскости, проходящей через некоторую точку с координатами (x₀,y₀,z₀), в общем виде записывается так:
A(x-x₀) + B(y-y₀) + C(z-z₀)= 0, где коэффициенты A,B,C - координаты вектора нормали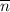
Найдём вектор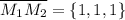
Вектор нормали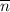 найдём из векторного произведения векторов a и M₁M₂
найдём из векторного произведения векторов a и M₁M₂
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему: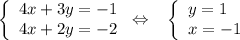
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Пусть z = -4
Снова решим систему: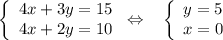
Координаты точки B(0, 5, -4)
Найдём направляющий вектор прямой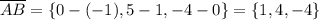
Запишем уравнение прямой в каноническом виде: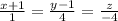
И в параметрическом виде: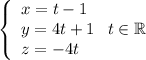
запишем ее в виде
то есть второй член тогда будет равен
Возьмем для начало такое число
то есть мы предположим что самое максимальное число заданными только 9
и их сумма уже будет равна 9*1000=9000, но возьмем еще 8 , для того что бы посмотреть максимальную сумму , 9*1008=9072
то есть видно что второе число уже будет грубо
ответ 9