1)
y = 0 - ось OXПлощадь фигуры будем искать на промежутке [0;3]
Т.к фигура расположена под осью OX, значит площадь фигуры находим по формуле
S =
Теперь просто подставляем значения
S = ед^2
2) Не совсем понял, решу позже
3)
Парабола пересекает ось OX в точках 1 и 4. Будем искать площадь на промежутке [1;4]
1)
y = 0 - ось OX
Площадь фигуры будем искать на промежутке [0;3]
Т.к фигура расположена под осью OX, значит площадь фигуры находим по формуле
S =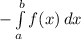
Теперь просто подставляем значения
S =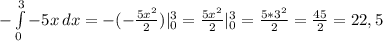 ед^2
ед^2
2) Не совсем понял, решу позже
3)
Парабола пересекает ось OX в точках 1 и 4. Будем искать площадь на промежутке [1;4]
S =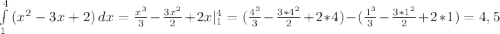 ед^2
ед^2