Пара́бола (греч. παραβολή — приложение) — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Наряду с эллипсом и гиперболой, парабола является коническим сечением.
Пошаговое объяснение:
Парабола — это график функции описанный формулой ax2+bx+c=0. Чтобы построить параболу нужно следовать простому алгоритму действий: 1 ) Формула параболы y=ax2+bx+c, если а>0 то ветви параболы направленны вверх, а<0 то ветви параболы направлены вниз. Свободный член c эта точке пересекается параболы с осью OY ... Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0; Виды уравнений: a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту; b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0: ax2+bx=0, х(ax+b)=0, х=0 и ax+b=0; c)Неполное квадратное уравнение вида ax2+c=0.
1. x∈( -∞;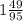 )
)
2.y∈(45;+∞)
4.b∈(4/11;+∞)
5.x∈[151\696;+∞)
Пошаговое объяснение:
1. 3,3x-1,6+1,2x<9,3+3,5-5x
3,3x+1,2x+5x<9,3+3,5+1,6
9,5x<14,4
x<144/95
x<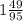
ответ: x∈( -∞;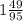 )
)
2.4,5y+9-3,1+3,1y>5,9+7,2y
4,5x+3,1y-7,2y>5,9+9+3,1
0,4y>18
y>45
ответ:y∈(45;+∞)
3.9(0,5у + 1) - 3,1(1 - у) > 5,9 + 7,2у;
0,6a-1,2-0,2-0,8a-1,6+3,5
Тут знак не стоит,не получится решить
4.0,6(а - 2) - 0,2 - 0,8(а + 2) + 3,5;
-1,4+5,5b-1<-5,5b+1,6
11b>4
b>4/11
ответ:b∈(4/11;+∞)
5.51 (14х – 3) »(18х - 2)
714x-153»18х - 2
696x»151
x»151\696
ответ:x∈[151\696;+∞)
Пара́бола (греч. παραβολή — приложение) — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Наряду с эллипсом и гиперболой, парабола является коническим сечением.
Пошаговое объяснение:
Парабола — это график функции описанный формулой ax2+bx+c=0. Чтобы построить параболу нужно следовать простому алгоритму действий: 1 ) Формула параболы y=ax2+bx+c, если а>0 то ветви параболы направленны вверх, а<0 то ветви параболы направлены вниз. Свободный член c эта точке пересекается параболы с осью OY ... Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0; Виды уравнений: a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту; b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0: ax2+bx=0, х(ax+b)=0, х=0 и ax+b=0; c)Неполное квадратное уравнение вида ax2+c=0.