Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
gazizkadyrzhan
25.08.2020 21:54 •
Математика
Вычислить предел (без лопиталя):
Показать ответ
Ответ:
Lidyanka
10.10.2020 12:23
По замечательному пределу
, следовательно, имеем
0,0
(0 оценок)
Популярные вопросы: Математика
timkalo
27.01.2022 14:35
Было 370 битона расыполи его по 9 мишком сколько было в 3 мишках её ришить...
7534558
27.01.2022 14:35
Перевод с татарского стих жейге болында...
VeNoM13371
27.01.2022 14:35
Вдоме, в ко¬то¬ром живёт женя, один подъезд. на каждом этаже по во¬семь квартир. женя живёт в квартире 87. на каком этаже живёт женя?...
mariyamariya201
27.01.2022 14:35
Решите уравнение 3 2/5: (5 3/14 -x)=2 1/10...
Даня1221
27.01.2022 14:35
Втрикутник авс(кут с=90 град.)гіпотенуза=12см.точка м рівновіддалена від вершин трикутн. на 10 см.знайти відстань від точки м до площини трикутника! )...
кристина2043
27.01.2022 14:35
Таймер в часах поставили так , что он подает один сигнал через каждые полчаса.в первый раз таймер просигналил в 13.30. во сколько он просигналит в седьмой раз...
yayy6uytuy6
27.01.2022 14:35
Для ремонта комнаты необходимо 16м55см бордюра для обоев.на сколько сантиметров надо укоротить бордюр длинной 17м,чтобы получить кусок нужной длины...
innahot418
27.01.2022 14:35
На 2 полках лежали книги на первой не известно ,а на второй в 3 раза больше чем на первой когда со второй полки на первую переложили 10 книг то стало поровну...
salhk
27.01.2022 14:35
Из ружья выстрелили 40 раз,не попали 4 раза.определите процент попаданий....
kri2221
27.01.2022 14:35
Из двух городов, расстояние между которыми 2400км, вылетели одновременно навстречу друг другу два самолета. скорость одного из них равна 350 км/ч, а другого-250км/ч....
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
По замечательному пределу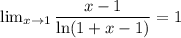 , следовательно, имеем
, следовательно, имеем