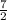Теперь запишем наш предел как произведение пределов (каждый из них, разумеется, существует): ; Первый из них - это первый замечательный предел. Имеем: . Теперь запишем разность косинусов как произведение синусов: ; Теперь каждый из пределов-сомножителей можно подогнать к замечательному пределу:
Домножим числитель и знаменатель на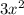 :
: 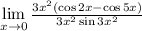
Теперь запишем наш предел как произведение пределов (каждый из них, разумеется, существует):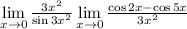 ; Первый из них - это первый замечательный предел. Имеем:
; Первый из них - это первый замечательный предел. Имеем: 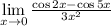 . Теперь запишем разность косинусов как произведение синусов:
. Теперь запишем разность косинусов как произведение синусов: 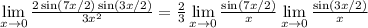 ; Теперь каждый из пределов-сомножителей можно подогнать к замечательному пределу:
; Теперь каждый из пределов-сомножителей можно подогнать к замечательному пределу:
ответ: