Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
ivannaprokuror
30.04.2023 14:43 •
Математика
Вычислить пределы, используя последствия первой и второй замечательных пределов и их последствия: 1) lim x->pi/2 (tg x/2)^(secx)
Показать ответ
Ответ:
Пес24
01.01.2021 01:04
Неопределенность
⇒ применяется второй замечательный предел.
0,0
(0 оценок)
Популярные вопросы: Математика
heylalaoxkpop
27.04.2022 23:38
Нужна по математики 11 класс...
Xaler
27.04.2022 23:38
Решить уравнения: 1. 2х – 12 = 6 + 4х; 2. 12 – 3х = 5 – 2х; 3. 5х – 3х + 6 = 1; Мне нужно именно решение и ответ...
андрей100500ый
24.12.2022 11:14
Люди кто может На изготовление 9 вечерних платьев требуется 37.35 м ткани. Сколько таких же вчерних платьев можно сшить из 83 м той же ткани?» Выясни, является ли зависимость между...
Волкова24
23.10.2020 20:42
507 ● а – 28785, якщо а=130....
Imdav88
21.08.2022 17:19
Назвить ортинату точки к [6.-8]...
ILLNNXSI
21.08.2022 17:19
Постройте на одной координатной прямой плоскости два графика прямой пропорциональности y=kx, один из которых проходит через точку А, а другой-через точку В. а) А (-2; 3), В (2; 3);...
масяня194
21.08.2022 17:19
Доброе утро, Что больше: 2 % от 6 или 6 % от с решением...
liliverbovetska
04.06.2021 01:19
График уравнения −6x+7y=41 проходит через точку A(−8b).Чему равно значение...
abdullaxadeaygün
13.02.2020 03:27
В одной и той же системе координат построим графики функции А)у=х б)у=2х в)у=-2х...
alena250880
31.08.2020 13:08
Укажите верное неравенство. А) 4,1 -4,8Б) -2,5 -3В) 10 -2,2Г)-7,6 -7,2...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Неопределенность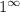 ⇒ применяется второй замечательный предел.
⇒ применяется второй замечательный предел.