Что мы будем использовать: последовательность монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
1) При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что Имеем:
2) При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что
Имеем:
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).
1000-7
993-7
986-7
979- 7
972-7
965-7
958-7
951-7
944-7
937-7
930-7
923-7
916-7
909-7
902-7
895-7
888-7
881-7
874-7
867-7
860-7
853-7
846-7
839-7
832-7
825-7
818-7
811-7
804-7
797-7
790-7
783-7
776-7
769-7
762-7
755-7
748-7
741-7
734-7
727-7
720-7
713-7
706-7
699-7
692-7
685-7
678-7
671-7
664-7
657-7
650-7
643-7
636-7
629-7
622-7
615-7
608-7
601-7
594-7
587-7
580-7
573-7
566-7
559-7
552-7
545-7
538-7
531-7
524-7
517-7
510-7
503-7
496-7
489-7
482-7
475-7
468-7
461-7
454-7
447-7
440-7
433-7
426-7
419-7
412-7
405-7
398-7
391-7
384-7
377-7
370-7
363-7
356-7
349-7
342-7
335-7
328-7
321-7
314-7
307-7
300-7
293-7
286-7
279-7
272-7
265-7
258-7
251-7
244-7
237-7
230-7
223-7
216-7
209-7
202-7
195-7
188-7
181-7
174-7
167-7
160-7
153-7
146-7
139-7
132-7
125-7
118-7
111-7
104-7
97-7
90-7
83-7
76-7
69-7
62-7
55-7
48-7
41-7
34-7
27-7
20-7
13-7
6-7
-1
Что мы будем использовать: последовательность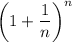
монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что
1)
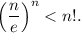При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 
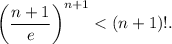Имеем:
2)
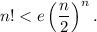При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что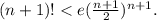 
Имеем:
Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).