Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
catcher1
23.01.2020 02:30 •
Математика
Вычислите не собственный интеграл или доказать его расходимость
Показать ответ
Ответ:
vipkakunina
09.10.2020 22:29
Поскольку несобственный интеграл
сходится, то сходиться будет интеграл
(первый признак сравнения).
0,0
(0 оценок)
Популярные вопросы: Математика
СВСЛ1
04.02.2021 01:33
решить номер 849. Известно ,что а больше b. Может ли разность a -b выражаться числом: -1,5;0;2,6?...
daniilmosl
19.07.2022 19:44
УМОЛЯЮ МЛЖЕТЕ В ТЕТРАДКЕ НАПИСАТЬ)...
Stella2002111
19.11.2020 23:25
6 Вычисли с проверкой. 83 600 : 76 576 000 : 16 68 441: 89 219 368 : 68 428 452 : 94 44 370:58 59 236:59 446 376:84 645 888 : 96 в столбик...
vlmx2freddy
25.05.2023 23:23
753. Обратите десятичную дробь в обыкновенную и найдите значе- ние выражения: ...
Efimenko34
31.08.2022 07:06
записывая квадрат двучлена в виде произведения двух членов осуществите умножение умножения в столбик...
paa050403
27.01.2023 07:29
3) (x + 3)2 + (4 - x)2 = 2(x – 4)(x + 3)....
настя7565
07.12.2020 22:11
Вычислить 8 целых 2/9 - 6 1/2...
врошдщ
23.10.2021 08:09
Какую дробь нельзя перевести к знаменателю 45...
svetiksemisvetik2004
10.10.2020 11:38
Из чисел −205,7; 205,11; −205,8; 205,19 наименьший модуль имеет число...
stregubkin
02.06.2020 16:30
Поанализируй и расскажи,какие датчики находятся ...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Поскольку несобственный интеграл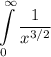 сходится, то сходиться будет интеграл
сходится, то сходиться будет интеграл 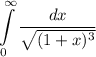 (первый признак сравнения).
(первый признак сравнения).