Эта дробь записывается в строчку. Например: 5,2. При произношении мы должны сказать не пять запятая два, а пять целых две десятых.
От количества цифр после запятой меняется произношение дроби.
5,2 - пять целых две десятых;
5,02 - пять целых две сотых;
5,002 - пять целых две тысячных;
5,0002 - пять целых две десятитысячных и т.д.
Обыкновенная дробь.
Эта дробь записывается дробью. Например: . При произношении мы должны сказать не пять дробь девять, а пять девятых. Если же перед дробью стоит целое число (например 3), то мы должны сказать две целых две третьих, и такая дробь называется смешанная.
243
14 17.3571428
-103
98
-50
42
-80
70
-100
98
-20
14
-60
56
-40
28
-120
112
8
6372 12
60 531
-37
36
-12
12
0
10914 34
102 321
71
68
-34
34
0
3912 12
36 326
-31
24
-72
72
0
6404 15
60 427
-40
30
-105
105
0
10104 12
96 842
-50
48
-24
24
0
394515
30 263
-94
90
-45
45
0
7 96515
75 531
-46
45
-15
15
0
Пошаговое объяснение:
Долго((
Десятичная дробь.
Эта дробь записывается в строчку. Например: 5,2. При произношении мы должны сказать не пять запятая два, а пять целых две десятых.
От количества цифр после запятой меняется произношение дроби.
5,2 - пять целых две десятых;
5,02 - пять целых две сотых;
5,002 - пять целых две тысячных;
5,0002 - пять целых две десятитысячных и т.д.
Обыкновенная дробь.
Эта дробь записывается дробью. Например: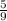 . При произношении мы должны сказать не пять дробь девять, а пять девятых. Если же перед дробью стоит целое число (например 3
. При произношении мы должны сказать не пять дробь девять, а пять девятых. Если же перед дробью стоит целое число (например 3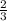 ), то мы должны сказать две целых две третьих, и такая дробь называется смешанная.
), то мы должны сказать две целых две третьих, и такая дробь называется смешанная.