иррациональные цисла - действительные не являющиеся рациональными...
доказать существование - достаточно привести пример.
Пример иррационального числа
понятно, что оно действительное (величина длины диагонали квадрата со стороной 1, например), покажем, что оно не является рациональным, то есть не существует дроби х/у=√2, где х - целое, у - натуральное
Предположим обратное, то есть такие х и у существуют, тогда
(самое сложное)
разложив на множители х и у получим:
слева в равенстве число 2 в нечетной степени (действительно один раз уже есть, и могут быть от у*у, но только в четных степенях, а один плюс четное - нечетно)
справа 2 если и есть то только в четной степени.
а 2 в нечетной степени не может быть равно 2 в четной
получили противоречие
Значит представления √2 в виде дроби не существует.
Таким образом число √2 - иррационально
P.S. использовано (два натуральных числа равны ⇔совпадают все степени простых сомножителей)
иррациональные цисла - действительные не являющиеся рациональными...
доказать существование - достаточно привести пример.
Пример иррационального числа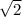
понятно, что оно действительное (величина длины диагонали квадрата со стороной 1, например), покажем, что оно не является рациональным, то есть не существует дроби х/у=√2, где х - целое, у - натуральное
Предположим обратное, то есть такие х и у существуют, тогда
(самое сложное)
разложив на множители х и у получим:
слева в равенстве число 2 в нечетной степени (действительно один раз уже есть, и могут быть от у*у, но только в четных степенях, а один плюс четное - нечетно)
справа 2 если и есть то только в четной степени.
а 2 в нечетной степени не может быть равно 2 в четной
получили противоречие
Значит представления √2 в виде дроби не существует.
Таким образом число √2 - иррационально
P.S. использовано (два натуральных числа равны ⇔совпадают все степени простых сомножителей)
task/29442811
Решить систему уравнений { x²+y² - xy =1 ; x+y = -2 . Вычислить 3xy .
Решение : { x²+y² - xy =1 ; x+y = -2.⇔ { (x+y)² - 3xy =1 ; x+y = -2.⇔
{ (-2)² - 3xy = 1 ; x+y = -2.⇔ { 4 - 1 = 3xy ; x+y = -2. ⇔{ 3xy = 3 ; x+y = -2. ⇔
{ xy = 1 ; x+y = - 2 .⇔ { x(-2-x) =1 ; y = 2 - x .⇔ { (x+1)² =0 ; y = 2 - x.⇔{x= -1 ; y=-1.
ответ: x= -1 ; y= - 1 ; 3xy =3
P.S.
{ xy = 1 ; x+y = - 2 x и y можно рассматривать как корни квадратного
уравнения t² + 2t +1=0 ( по обратной теореме Виета)
(t+1)² =0 ⇒ t = -1 * * * t ₁ = t₂ = -1 * * *