В 9 раз
Пошаговое объяснение:
Для начала поймём, чему равна площадь круга
S = πR²
Для вычисление площадей нужны радиусы, находим
Второй радиус известен, нужен первый
1) 18/2 = 9 - Радиус первого круга
Ищем площади, за число π берём 3,14:
2) 3,14 * 9 * 9 = 254,34 - Площадь первого круга
3) 3,14 * 3 * 3 = 28,26 - Площадь второго
4) = 9 - отношение площадей окружностей
Но можно было сделать проще, без вычислений площадей
1) Так как мы знаем чему равна площадь окружности, можно было Её не вычислять, а сразу искать отношение
Числа π сокращаются, а радиусы сначала вычисляются и тоже сокращаются
Получаем выражение
9 сокращаем с 3
Получаем
В данном случаи не нужен калькулятор, но если в задании указано найти площадь, а не только соотношение, то этот не подойдёт
Прямая, которая задается уравнением , можно переписать в виде функции , где
Определим формулу линейной функции, которая проходит через две точки: и
Для этого подставим соответствующие координаты точек в функцию и получим систему из двух линейных уравнений:
Из первого уравнения подставим во второе уравнение:
Тогда
Получили линейную функцию, которая задается формулой
Для проверки того, проходит ли прямая через заданную точку, следует подставить координаты этой точки в функцию и посмотреть результат.
а) Для точки :
— правда
б) Для точки :
— неправда
ответ: а) да; б) нет.
В 9 раз
Пошаговое объяснение:
Для начала поймём, чему равна площадь круга
S = πR²
Для вычисление площадей нужны радиусы, находим
Второй радиус известен, нужен первый
1) 18/2 = 9 - Радиус первого круга
Ищем площади, за число π берём 3,14:
2) 3,14 * 9 * 9 = 254,34 - Площадь первого круга
3) 3,14 * 3 * 3 = 28,26 - Площадь второго
4)
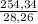= 9 - отношение площадей окружностей
Но можно было сделать проще, без вычислений площадей
1) Так как мы знаем чему равна площадь окружности, можно было Её не вычислять, а сразу искать отношение
Числа π сокращаются, а радиусы сначала вычисляются и тоже сокращаются
Получаем выражение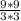
9 сокращаем с 3
Получаем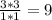
В данном случаи не нужен калькулятор, но если в задании указано найти площадь, а не только соотношение, то этот не подойдёт
Прямая, которая задается уравнением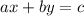
, можно переписать в виде функции 
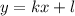, где 
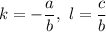
Определим формулу линейной функции, которая проходит через две точк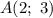и:
и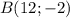 
Для этого подставим соответствующие координаты точек в функцию и получим систему из двух линейных уравнений:
Из первого уравнения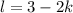
подставим во второе уравнение:
Тогда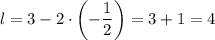
Получили линейную функцию, которая задается формулой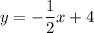
Для проверки того, проходит ли прямая через заданную точку, следует подставить координаты этой точки в функцию и посмотреть результат.
а) Для точки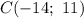
:
б) Для точки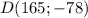
:
ответ: а) да; б) нет.