1) Т.к. 9 часов длится стоянка, то в движении теплоход был 33 - 9 = 24 (ч).
2) Пусть t (ч.) теплоход двигался по течению. Если объект движется по течению, то его скорость увеличивается на скорость течения, т.е. 24 + 4 = 28 (км/ч) - скорость теплохода по течению, а путь составляет 28*t (км)
3) Против течения теплоход двигался (24 - t) (ч.) со скоростью 24 - 4 = 20(км/ч), тогда весь обратный путь составляет 20*(24 - t) (км).
4) Т.к. расстояние от исходного пункта до стоянки и от стоянки до исходного одно и то же, то составим уравнение:
28t = 20(24 - t)
28t = 480 - 20t
28t + 20t = 480
48t = 480
t = 10 (ч)
Путь от исходного пункта до стоянки: 28*10 = 280 (км), обратно -- то же расстояние, т.е. за рейс теплоход км)
560 км
Пошаговое объяснение:
1) Т.к. 9 часов длится стоянка, то в движении теплоход был 33 - 9 = 24 (ч).
2) Пусть t (ч.) теплоход двигался по течению. Если объект движется по течению, то его скорость увеличивается на скорость течения, т.е. 24 + 4 = 28 (км/ч) - скорость теплохода по течению, а путь составляет 28*t (км)
3) Против течения теплоход двигался (24 - t) (ч.) со скоростью 24 - 4 = 20(км/ч), тогда весь обратный путь составляет 20*(24 - t) (км).
4) Т.к. расстояние от исходного пункта до стоянки и от стоянки до исходного одно и то же, то составим уравнение:
28t = 20(24 - t)
28t = 480 - 20t
28t + 20t = 480
48t = 480
t = 10 (ч)
Путь от исходного пункта до стоянки: 28*10 = 280 (км), обратно -- то же расстояние, т.е. за рейс теплоход км)
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ: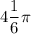 ;
;