Будем использовать формулу Эйлера:
И по формуле бинома Ньютона
Аналогично для также делается как и с синусом.
Будем использовать формулу Эйлера:
И по формуле бинома Ньютона
Аналогично для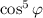 также делается как и с синусом.
также делается как и с синусом.