Высота правильной треугольной пирамиды равна 40 см, а угол, который образует апофема с плоскостью основания пирамиды, равен 30°. Вычисли объём пирамиды.

Предположим, что х принадлежит множеству целых чисел.                           решаем первое неравенство.     -5< x-2< 5         -3< x< 7, т е   х принадлежит промежутку (-3; 7),   который содержит  9 целых чисел, крайние не включены, т к неравенство строгое.                                                 решаем второе неравенство     x^2 > 16.решением является объединение двух промежутков   х < -4 и  x> 4.       благоприятными событиями является выбор из девяти   решений   первого неравенства, которые также являются решениями и второго (их  пересечение). это решения   5,   6,.7.   вероятность -- это отношение благоприятных исходов( 3 ) к ко всем возможным   (9), значит она равна   3/9=1/3

ответ:  180.  

Вот формула площади трапеции:

, где a и b - основания трапеции, а h - высота (S, разумеется, площадь).

Вот только одна проблема: мы не знаем высоты. Но чтобы ее узнать, можно отсечь от трапеции (например, справа) прямоугольный треугольник. Его гипотенуза (c)- это боковая сторона трапеции, которая равна 13. Нижний катет (b) будет равен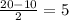 . Почему - можно увидеть на рисунке ниже. Второй катет этого треугольника (а) - это и есть высота, которую можно найти по теореме Пифагора:  

Теперь высоту мы знаем и можем найти площадь трапеции:

Задача решена!