Математика: (x+1)^n/3^(n+1) Знайти радіус збіжності ряду

ответ: Пошаговое объяснение:Пусть: Тогда уравнение принимает вид: Заметим, что если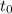 корень уравнения 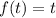, то он и корень уравнения: , действительно:Найдем все такие корни: Заметим, что функция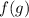 - монотонно возрастает. Предположим, что в уравнении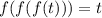 существует корень 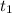, такой, что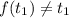 Рассмотрим случай: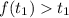 . Поскольку,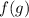 - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: , то верно и данное неравенство: 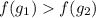Из данного утверждения следует, что :Но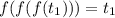 , то есть мы пришли...

(x+1)^n/3^(n+1) Знайти радіус збіжності ряду

Показать ответ

Ответ:

ksuvladyckina16

24.12.2020 12:49

ответ: x=-2

Пошаговое объяснение:

$\sqrt{12+\sqrt{12+\sqrt[]{20+4x+x^2} } } =x^2+4x+8\\x^2+4x+8 = (x+2)^2+4 = t\geq4 \\\sqrt{12+\sqrt{12+\sqrt[]{12+t} } } = t$

Пусть:

$f(g) =\sqrt{12+g}$

Тогда уравнение принимает вид:

f(f(f(t))) = t

Заметим, что если $t_{0}$ корень уравнения f(t) = t , то он и корень уравнения:

f(f(f(t))) = t , действительно:

$f(t_{0} ) = t_{0}\\f(f(t_{0})) = f(t_{0}) =t_{0}\\f(f(f(t_{0})))= f(f(t_{0}))= t_{0}$

Найдем все такие корни:

$\sqrt{12+t} =t\\t\geq0 \\12+t =t^2\\t^2-t-12=0\\t_{1} =4\\t_{2} =-3$

Заметим, что функция f(g) - монотонно возрастает.

Предположим, что в уравнении f(f(f(t))) = t существует корень $t_{1}$ , такой, что $f(t_{1} } )\neq t_{1}$

Рассмотрим случай: $f(t_{1} }) t_{1}$ .

Поскольку, f(g) - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: $g_{1} g_{2}$ , то верно и данное неравенство: $f(g_{1} )f(g_{2} )$

Из данного утверждения следует, что :

$f(f(t_{1} })) f(t_{1})t_{1}\\f(f(f(t_{1} }))) f(f(t_{1}))f(t_{1})t_{1}$

Но $f(f(f(t_{1} }))) =t_{1}$ , то есть мы пришли к противоречию.

Аналогично показывается невозможность утверждения для случая

$f(t_{1} })$ . Таким образом, других корней помимо x=-2 нет.

0,0(0 оценок)

Ответ:

Drftdsrx

19.08.2022 21:46

1-й

1) Пусть S - расстояние от причала до места, где катер догонит лодку.
9 + 3 - скорость лодки, идущее вниз по течению.
21 + 3 - скорость катера, идущего вниз по течению.
S/(9+3) - время, за которое лодка дойдёт до места, в котором катер догонит лодку.
S/(21+3) - время, за которое катер дойдёт до места, в котором он догонит лодку.
Поскольку лодка находилась в пути на 2 часа дольше, чем катер, можно составить уравнение:
S/(9+3) - S/(21+3) = 2
S/12 - S/24 = 2
2S/24 - S/24 = 2
S/24 = 2
S = 2 • 24
S = 48 км - расстояние от причала до места, где катер догонит лодку.
2) 48 : 24 = 2 часа должен идти катер до места, где он догонит лодку.
3) 10 + 2 = 12 часов - время, в которое катер отошел от причала.
4) 12 + 2 = 14 часов - время, в которое катер догонит лодку.
ответ: 14 часов

ПРОВЕРКА
(9+3) • (2+2) = (21+3) • 2
12 • 4 = 24 • 2
48 = 48

Или
2-й

1) Пусть t - время, через которое катер догонит лодку
t+2 - время, которое лодка находится в пути, пока ее не догонит катер.
(21+3) - (9+3) - скорость, с которой расстояние между лодкой и катером сокращается.
(t+2)(9+3)) = t(21+3)
(t+2)• 12 = t • 24
t + 2 = t • 24 / 12
t + 2 = 2t
2t - t = 2
t = 2 часа - время, через которое катер догонит лодку.
2) 10 + 2 = 12 часов - время, в которое катер отошел от причала.
3) 12 + 2 = 14 часов - время, в которое катер догонит лодку.

0,0(0 оценок)

Популярные вопросы: Математика