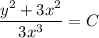Умножим дифференциальное уравнение на интегрирующий множитель . Тогда уравнение примет вид
Заметим, что , т.е. дифференциальное уравнение является уравнением в полных дифференциалах.
Интегрируем функцию F сначала по х:
Теперь продифференцируем по переменной у:
. Действительно, . Отсюда
Общий интеграл:
Умножим дифференциальное уравнение на интегрирующий множитель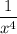 . Тогда уравнение примет вид
. Тогда уравнение примет вид
Заметим, что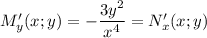 , т.е. дифференциальное уравнение является уравнением в полных дифференциалах.
, т.е. дифференциальное уравнение является уравнением в полных дифференциалах.
Интегрируем функцию F сначала по х: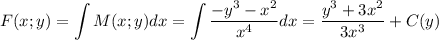
Теперь продифференцируем по переменной у:
Общий интеграл: