Чтобы найти промежутки монотонности, найдём точки смены монотонности. Они достигаются при равенстве производной нулю. Решим соответствующее уравнение:
⇔ или .
Так мы получили точки смены монотонности. Очевидно, что функция возрастает на промежутке (-∞;) - это легко показать на конкретных значениях, а значит можно восстановить все остальные промежутки так, как показано в ответе.
Возрастает на (-∞;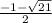 ), дальше убывает на (
), дальше убывает на (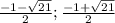 ) и снова возрастает на (
) и снова возрастает на (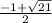 ;+∞).
;+∞).
Пошаговое объяснение:
Найдём производную исходной функции, пользуясь правилами дифференцирования:
Чтобы найти промежутки монотонности, найдём точки смены монотонности. Они достигаются при равенстве производной нулю. Решим соответствующее уравнение:
Так мы получили точки смены монотонности. Очевидно, что функция возрастает на промежутке (-∞;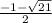 ) - это легко показать на конкретных значениях, а значит можно восстановить все остальные промежутки так, как показано в ответе.
) - это легко показать на конкретных значениях, а значит можно восстановить все остальные промежутки так, как показано в ответе.